
如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交 轴
轴
于 两点,点
两点,点 在⊙
在⊙ 上.
上.

(1)求出 两点的坐标;
两点的坐标;
(2)试确定经过A、B且以点P为顶点的抛物线解析式;
(3)在该抛物线上是否存在一点 ,使线段
,使线段 与
与 互相平分?若存在,求出点
互相平分?若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(1) ,
,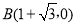 (2)
(2)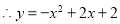 或
或 (3)存在
(3)存在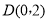 使线段
使线段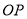 与
与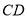 互相平分
互相平分
【解析】
试题分析:(1)作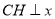 轴,
轴,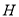 为垂足,连接CB,根据C点的坐标及圆的半径可求得HB=
为垂足,连接CB,根据C点的坐标及圆的半径可求得HB=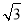 ,从而根据坐标的特点求出A、B的坐标;
,从而根据坐标的特点求出A、B的坐标;
(2)根据圆的对称性(垂径定理)和抛物线的对称性可求得P点的坐标(1,3)(1,-1),分别设出顶点式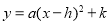 ,然后代入A、B点的坐标即可求得解析式;
,然后代入A、B点的坐标即可求得解析式;
(3)根据题意假设存在D点,则由题意知四边形 是平行四边形,根据平行四边形的性质得PC=OD,且PC∥OD,又由图形可知PC∥y轴,判断出D在y轴上,因此可由PC=2可求得OD=2,因此可得D点的坐标,代入二次函数的解析式可判断存在这样的点D(0,2).
是平行四边形,根据平行四边形的性质得PC=OD,且PC∥OD,又由图形可知PC∥y轴,判断出D在y轴上,因此可由PC=2可求得OD=2,因此可得D点的坐标,代入二次函数的解析式可判断存在这样的点D(0,2).
试题解析:【解析】
(1)作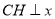 轴,
轴,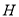 为垂足,连接CB.
为垂足,连接CB.
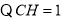 ,半径
,半径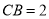
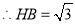 ,
,
故 ,
,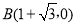

(2)由圆与抛物线的对称性可知抛物线的顶点 的坐标为
的坐标为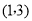 或(1,
或(1,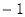 ),
),
设抛物线表达式 ,
,
把点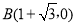 代入上式,解得
代入上式,解得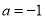
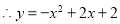 .
.

设抛物线解析式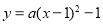 ,
,
把点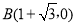 代入上式,解得a=
代入上式,解得a=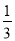 ,
,

 .
.

(3)假设存在点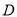 使线段
使线段 与
与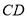 互相平分,
互相平分,
则四边形 是平行四边形
是平行四边形
 且
且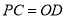 .
.
 轴,
轴,
 点
点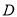 在
在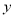 轴上.
轴上.
又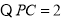 ,
,
 ,
,
即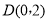 或(0,-2).
或(0,-2).
(0,2)满足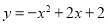 ,
,
(0,-2)不满足 ,
,
 点
点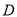 (0,2)在抛物线上.
(0,2)在抛物线上.
所以存在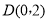 使线段
使线段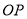 与
与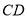 互相平分.
互相平分.
考点:待定系数法,二次函数的图像与性质,平行四边形的性质


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源:2014-2015学年北京市海淀区九年级上学期期末考试数学试卷(解析版) 题型:解答题
某工厂生产的某种产品按质量分为10个档次,据调研显示,每个档次的日产量及相应的单件利润如下表所示(其中x为正整数,且1≤x≤10):

为了便于调控,此工厂每天只生产一个档次的产品.当生产质量档次为x的产品时,当天的利润为y万元.
(1)求y关于x的函数关系式;
(2)工厂为获得最大利润,应选择生产哪个档次的产品?并求出当天利润的最大值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市丰台区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,A,B,C是⊙O上的三个点,如果∠BAC=30°,那么∠BOC的度数是( )

A.60° B.45° C.30° D.15°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1,C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A( ,0),B(0,4),则点B4的坐标为 ,点B2014的坐标为 .
,0),B(0,4),则点B4的坐标为 ,点B2014的坐标为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市东城区九年级上学期期末考试数学试卷(解析版) 题型:选择题
如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
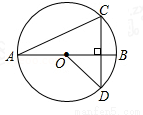
A.120° B.140° C.150° D.160°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市大兴区九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知:如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠D=150°,四边形的周长为32,求BC和DC的长.

查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市朝阳区九年级上学期期末考试数学试卷(解析版) 题型:解答题
随着“节能减排、绿色出行”的健康生活意识的普及,新能源汽车越来越多地走进百姓的生活.某汽车租赁公司拥有40辆电动汽车,据统计,当每辆车的日租金为120元时,可全部租出;当每辆车的日租金每增加5元时,未租出的车将增加1辆;该公司平均每日的各项支出共2100元.
(1)若某日共有x辆车未租出,则当日每辆车的日租金为 元;
(2)当每辆车的日租金为多少时,该汽车租赁公司日收益最大?最大日收益是多少?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年北京市昌平区九年级上学期期末考试数学试卷(解析版) 题型:选择题
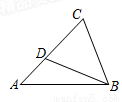
如图,在△ABC中,D为AC边上一点,若∠DBC=∠A,BC= ,AC=3,则CD的长为( )
,AC=3,则CD的长为( )
A.1 B. C.2 D.
C.2 D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com