
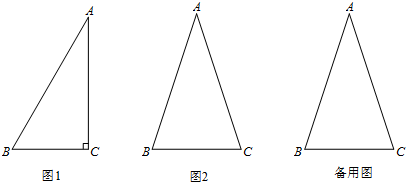
分析 (1)根据等腰三角形的性质,求出底角的度数,判断出三角形为等边三角形,再根据正对的定义解答进而得出sad90°的值;
(2)求出0度和180度时等腰三角形底和腰的比即可;
(3)过点B作BD⊥AC于点D,利用勾股定理即可解答;
(4)作出等腰△ABC,构造等腰三角形BCD,根据正对的定义解答.
解答 解:(1)根据正对定义,
当顶角为60°时,等腰三角形底角为60°,
则三角形为等边三角形,
则sad60°=$\frac{1}{1}$=1.
故答案为:1;
(2)当∠A接近0°时,sadA接近0,
当∠A接近180°时,等腰三角形的底接近于腰的二倍,故sadA接近2.
于是sadA的取值范围是0<sadA<2.
故答案为:0<sadA<2.
(3)如图2,过点B作BD⊥AC于点D.
∴∠ADB=∠CDB=90°.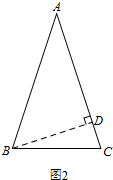
在Rt△ADB中,tanA=$\frac{3}{4}$,
∴设BD=3k,则AD=4k.
∴AB=$\sqrt{B{D^2}+A{D^2}}=5k$.
∵AB=AC,
∴CD=k.
∴在Rt△CDB中,利用勾股定理得,BC=$\sqrt{10}k$.
在等腰△ABC中,sad A=$\frac{BC}{AB}=\frac{{\sqrt{10}k}}{5k}=\frac{{\sqrt{10}}}{5}$.
(4)如图3所示:已知:∠A=36°,AB=AC,BC=BD,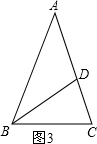
∴∠A=∠CBD=36°,∠ABC=∠C=72°,
∴△BCD∽△ABC,
∴$\frac{BC}{AC}=\frac{CD}{BC}$,
∴$\frac{BC}{BC+CD}=\frac{CD}{BC}$,
解得:BC=$\frac{\sqrt{5}+1}{2}$CD,
∴sad36°=$\frac{CD}{BC}=\frac{\sqrt{5}-1}{2}$.
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查了解直角三角形:利用三角函数的定义和相似三角形的判定与性质,根据题意得出BC与CD的关系是解题关键.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
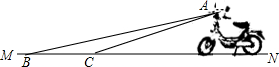 齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)
齐河路路通电动车厂新开发的一种电动车如图,它的大灯A射出的光线AB,AC 与地面MN 所夹的锐角分别为8°和10°,大灯A与地面的距离为1m则该车大灯照亮地面的宽度BC是1.4m.(不考虑其它因素)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
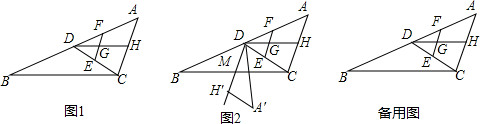 如图1,在△ABC中,CD为AB边上的中线,点E、F分别在线段CD、AD上,且$\frac{DF}{DB}=\frac{DE}{DC}$.点G是EF的中点,射线DG交AC于点H.
如图1,在△ABC中,CD为AB边上的中线,点E、F分别在线段CD、AD上,且$\frac{DF}{DB}=\frac{DE}{DC}$.点G是EF的中点,射线DG交AC于点H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com