
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌвдACЮЊжБОЖзїЁбOЃЌНЛABгкDЃЌЙ§ЕуOзїOEЁЮABЃЌНЛBCгкEЃЎ
ЃЈ1ЃЉЧѓжЄЃКEDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШчЙћЁбOЕФАыОЖЮЊ![]() ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ
ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШСЌНгODЃЌгЩOEЁЮABЃЌИљОнЦНааЯпгыЕШбќШ§НЧаЮЕФаджЪЃЌвзжЄЕУ![]() Ёе
Ёе![]() МДПЩЕУ
МДПЩЕУ![]() ЃЌдђПЩжЄЕУ
ЃЌдђПЩжЄЕУ![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгCDЃЌИљОнжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЌМДПЩЕУ![]() РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ
РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ![]() ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ
ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ![]() ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ
ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ![]() ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ
ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ![]() гы
гы![]() ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЪдЬтНтЮіЃК(1)жЄУїЃКСЌНгODЃЌ
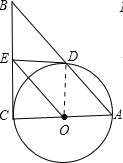
ЁпOEЁЮABЃЌ
ЁрЁЯCOE=ЁЯCADЃЌЁЯEOD=ЁЯODAЃЌ
ЁпOA=OD,
ЁрЁЯOAD=ЁЯODAЃЌ
ЁрЁЯCOE=ЁЯDOEЃЌ
дкЁїCOEКЭЁїDOEжаЃЌ
 ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
![]()
ЁрEDЁЭODЃЌ
ЁрEDЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
(2)СЌНгCDЃЌНЛOEгкMЃЌ
дкRtЁїODEжаЃЌ
ЁпOD=32ЃЌDE=2ЃЌ
![]()
ЁпOEЁЮABЃЌ
ЁрЁїCOEЁзЁїCABЃЌ
![]() ЁрAB=5ЃЌ
ЁрAB=5ЃЌ
ЁпACЪЧжБОЖЃЌ
![]()
![]()
![]()
![]()
ЁпEFЁЮABЃЌ
![]()
![]()
![]()
ЁрSЁїADF=SЬнаЮABEFSЬнаЮDBEF
![]()
ЁрЁїADFЕФУцЛ§ЮЊ![]()

ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПЁОЬтФПЁПвбжЊЃЌХзЮяЯпy=ax2+ax+bЃЈaЁй0ЃЉгыжБЯпy=2x+mгавЛИіЙЋЙВЕуMЃЈ1ЃЌ0ЃЉЃЌЧвaЃМbЃЎ
ЃЈ1ЃЉЧѓbгыaЕФЙиЯЕЪНКЭХзЮяЯпЕФЖЅЕуDзјБъЃЈгУaЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉжБЯпгыХзЮяЯпЕФСэЭтвЛИіНЛЕуМЧЮЊNЃЌЧѓЁїDMNЕФУцЛ§гыaЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉa=Љ1ЪБЃЌжБЯпy=Љ2xгыХзЮяЯпдкЕкЖўЯѓЯоНЛгкЕуGЃЌЕуGЁЂHЙигкдЕуЖдГЦЃЌЯжНЋЯпЖЮGHбиyжсЯђЩЯЦНвЦtИіЕЅЮЛЃЈtЃО0ЃЉЃЌШєЯпЖЮGHгыХзЮяЯпгаСНИіВЛЭЌЕФЙЋЙВЕуЃЌЪдЧѓtЕФШЁжЕЗЖЮЇЃЎ

ЁОД№АИЁПЃЈ1ЃЉb=Љ2aЃЌЖЅЕуDЕФзјБъЮЊЃЈЉ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЛЃЈ2ЃЉ
ЃЉЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ 2ЁмtЃМ
ЃЛЃЈ3ЃЉ 2ЁмtЃМ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉАбMЕузјБъДњШыХзЮяЯпНтЮіЪНПЩЕУЕНbгыaЕФЙиЯЕЃЌПЩгУaБэЪОГіХзЮяЯпНтЮіЪНЃЌЛЏЮЊЖЅЕуЪНПЩЧѓЕУЦфЖЅЕуDЕФзјБъЃЛ
ЃЈ2ЃЉАбЕу![]() ДњШыжБЯпНтЮіЪНПЩЯШЧѓЕУmЕФжЕЃЌСЊСЂжБЯпгыХзЮяЯпНтЮіЪНЃЌЯћШЅyЃЌПЩЕУЕНЙигкxЕФвЛдЊЖўДЮЗНГЬЃЌПЩЧѓЕУСэвЛНЛЕуNЕФзјБъЃЌИљОнa<bЃЌХаЖЯa<0ЃЌШЗЖЈDЁЂMЁЂNЕФЮЛжУЃЌЛЭМ1ЃЌИљОнУцЛ§КЭПЩЕУ
ДњШыжБЯпНтЮіЪНПЩЯШЧѓЕУmЕФжЕЃЌСЊСЂжБЯпгыХзЮяЯпНтЮіЪНЃЌЯћШЅyЃЌПЩЕУЕНЙигкxЕФвЛдЊЖўДЮЗНГЬЃЌПЩЧѓЕУСэвЛНЛЕуNЕФзјБъЃЌИљОнa<bЃЌХаЖЯa<0ЃЌШЗЖЈDЁЂMЁЂNЕФЮЛжУЃЌЛЭМ1ЃЌИљОнУцЛ§КЭПЩЕУ![]() ЕФУцЛ§МДПЩЃЛ
ЕФУцЛ§МДПЩЃЛ
ЃЈ3ЃЉЯШИљОнaЕФжЕШЗЖЈХзЮяЯпЕФНтЮіЪНЃЌЛГіЭМ2ЃЌЯШСЊСЂЗНГЬзщПЩЧѓЕУЕБGHгыХзЮяЯпжЛгавЛИіЙЋЙВЕуЪБЃЌtЕФжЕЃЌдйШЗЖЈЕБЯпЖЮвЛИіЖЫЕудкХзЮяЯпЩЯЪБЃЌtЕФжЕЃЌПЩЕУЃКЯпЖЮGHгыХзЮяЯпгаСНИіВЛЭЌЕФЙЋЙВЕуЪБtЕФШЁжЕЗЖЮЇЃЎ
ЪдЬтНтЮіЃК(1)ЁпХзЮяЯп![]() гавЛИіЙЋЙВЕуM(1,0)ЃЌ
гавЛИіЙЋЙВЕуM(1,0)ЃЌ
Ёрa+a+b=0ЃЌМДb=2aЃЌ
![]()
ЁрХзЮяЯпЖЅЕуDЕФзјБъЮЊ![]()
(2)ЁпжБЯпy=2x+mОЙ§ЕуM(1,0)ЃЌ
Ёр0=2ЁС1+mЃЌНтЕУm=2ЃЌ
Ёрy=2x2ЃЌ
дђ![]()
ЕУ![]()
Ёр(x1)(ax+2a2)=0,
НтЕУx=1Лђ![]()
ЁрNЕузјБъЮЊ![]()
Ёпa<bЃЌМДa<2aЃЌ
Ёрa<0ЃЌ
ШчЭМ1ЃЌЩшХзЮяЯпЖдГЦжсНЛжБЯпгкЕуEЃЌ
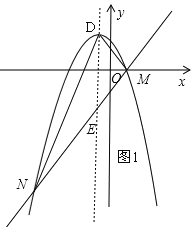
ЁпХзЮяЯпЖдГЦжсЮЊ![]()
![]()
![]()
ЩшЁїDMNЕФУцЛ§ЮЊSЃЌ
![]()
(3)ЕБa=1ЪБЃЌ
ХзЮяЯпЕФНтЮіЪНЮЊЃК![]()
га![]()
![]()
НтЕУЃК![]()
ЁрG(1,2)ЃЌ
ЁпЕуGЁЂHЙигкдЕуЖдГЦЃЌ
ЁрH(1,2)ЃЌ
ЩшжБЯпGHЦНвЦКѓЕФНтЮіЪНЮЊЃКy=2x+tЃЌ
x2x+2=2x+tЃЌ
x2x2+t=0ЃЌ
Ёї=14(t2)=0ЃЌ
![]() ЕБЕуHЦНвЦКѓТфдкХзЮяЯпЩЯЪБ,зјБъЮЊ(1,0)ЃЌ
ЕБЕуHЦНвЦКѓТфдкХзЮяЯпЩЯЪБ,зјБъЮЊ(1,0)ЃЌ
Аб(1,0)ДњШыy=2x+tЃЌ
t=2ЃЌ
ЁрЕБЯпЖЮGHгыХзЮяЯпгаСНИіВЛЭЌЕФЙЋЙВЕу,tЕФШЁжЕЗЖЮЇЪЧ![]()


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэЪЧМбМбЭљаЁвЬМвДђГЄЭОЕчЛАЕФМИДЮЪеЗбБъзММЧТМЃК
ЛиД№ЯТСаЮЪЬтЃК
ЪБМф | 1 | 2 | 3 | 4 | 5 | 6 | 7 | Ё |
ЕчЛАЗб | 0.6 | 1.2 | 1.8 | 2.4 | 3.0 | 3.6 | 4.2 | Ё |
ЃЈ1ЃЉЩЯБэЗДгГСЫБфСП КЭ жЎМфЕФЙиЯЕ, здБфСПЪЧ ,вђБфСПЪЧ .
ЃЈ2ЃЉАяжњМбМбдЄВтвЛЯТЃЌШчЙћЫ§ДђЕчЛАгУЕФЪБМфЪЧ10ЗжжгЃЌашвЊИЖ дЊЕчЛАЗбЃЛ
ЃЈ3ЃЉЧыФуаДГіЭЈЛАЪБМф![]() ЃЈЗжжгЃЉЃЈ
ЃЈЗжжгЃЉЃЈ![]() ЮЊе§ећЪ§ЃЉгыЫљвЊИЖЕФЕчЛАЗб
ЮЊе§ећЪ§ЃЉгыЫљвЊИЖЕФЕчЛАЗб![]() ЃЈдЊЃЉжЎМфЕФЙиЯЕЪН.
ЃЈдЊЃЉжЎМфЕФЙиЯЕЪН.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯпl1ЁЮl2ЃЌl3ЁЂl4КЭl1ЁЂl2ЗжБ№НЛгкЕуAЁЂBЁЂCЁЂDЃЌЕуPдкжБЯпl3Лђl4ЩЯЧвВЛгыЕуAЁЂBЁЂCЁЂDжиКЯЃЎМЧЁЯAEPЃНЁЯ1ЃЌЁЯPFBЃНЁЯ2ЃЌЁЯEPFЃНЁЯ3ЃЎ



(1)ШєЕуPдкЭМ(1)ЮЛжУЪБЃЌЧѓжЄЃКЁЯ3ЃНЁЯ1ЃЋЁЯ2ЃЛ
(2)жјЕуPдкЭМ(2)ЮЛжУЪБЃЌЧыаДГіЁЯ1ЁЂЁЯ2ЁЂЁЯ3жЎМфЕФЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
(3)ШєЕуPдкЭМ(3)ЮЛжУЪБЃЌаДГіЁЯ1ЁЂЁЯ2ЁЂЁЯ3жЎМфЕФЙиЯЕ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПAЁЂBСНСОЦћГЕЭЌЪБДгЯрОр330ЧЇУзЕФМзЁЂввСНЕиЯрЯђЖјааЃЌsЃЈЧЇУзЃЉБэЪОЦћГЕгыМзЕиЕФОрРыЃЌtЃЈЗжЃЉБэЪОЦћГЕааЪЛЕФЪБМфЃЌШчЭМЃЌL1ЃЌL2ЗжБ№БэЪОСНСОЦћГЕЕФsгыtЕФЙиЯЕЃЎ
ЃЈ1ЃЉL1БэЪОФФСОЦћГЕЕНМзЕиЕФОрРыгыааЪЛЪБМфЕФЙиЯЕЃП
ЃЈ2ЃЉЦћГЕBЕФЫйЖШЪЧЖрЩйЃП
ЃЈ3ЃЉЧѓL1ЃЌL2ЗжБ№БэЪОЕФСНСОЦћГЕЕФsгыtЕФЙиЯЕЪНЃЎ
ЃЈ4ЃЉ2аЁЪБКѓЃЌСНГЕЯрОрЖрЩйЧЇУзЃП
ЃЈ5ЃЉааЪЛЖрГЄЪБМфКѓЃЌAЁЂBСНГЕЯргіЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕу![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧЕШБп
ЗжБ№ЪЧЕШБп![]() ИїБпЩЯЕФЕуЃЌЧв
ИїБпЩЯЕФЕуЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ![]() ЃЉЧѓжЄЃК
ЃЉЧѓжЄЃК![]() ЪЧЕШБпШ§НЧаЮЃЎ
ЪЧЕШБпШ§НЧаЮЃЎ
ЃЈ![]() ЃЉШє
ЃЉШє![]() ЃЌЧѓЕШБп
ЃЌЧѓЕШБп![]() ЕФжмГЄЃЎ
ЕФжмГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌABЃН4![]() ЃЌACЁЭABЃЌBDЁЭABЃЌACЃНBDЃН3
ЃЌACЁЭABЃЌBDЁЭABЃЌACЃНBDЃН3![]() ЃЎЕу P дкЯпЖЮ AB ЩЯвд 1
ЃЎЕу P дкЯпЖЮ AB ЩЯвд 1![]() ЕФЫйЖШгЩЕу A ЯђЕу B дЫЖЏЃЌЭЌЪБЃЌЕу Q дкЯпЖЮ BD ЩЯгЩЕу B ЯђЕу D дЫЖЏЃЎЫќУЧдЫЖЏЕФЪБМфЮЊ
ЕФЫйЖШгЩЕу A ЯђЕу B дЫЖЏЃЌЭЌЪБЃЌЕу Q дкЯпЖЮ BD ЩЯгЩЕу B ЯђЕу D дЫЖЏЃЎЫќУЧдЫЖЏЕФЪБМфЮЊ ![]() ЃЈsЃЉЃЎ
ЃЈsЃЉЃЎ
ЃЈ1ЃЉШєЕу Q ЕФдЫЖЏЫйЖШгыЕу P ЕФдЫЖЏЫйЖШЯрЕШЃЌЕБ![]() ЃН1 ЪБЃЌЁїACP гыЁїBPQ ЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЌ ВЂХаЖЯДЫЪБЯпЖЮ PC КЭЯпЖЮ PQ ЕФЮЛжУЙиЯЕЃЛ
ЃН1 ЪБЃЌЁїACP гыЁїBPQ ЪЧЗёШЋЕШЃЌЧыЫЕУїРэгЩЃЌ ВЂХаЖЯДЫЪБЯпЖЮ PC КЭЯпЖЮ PQ ЕФЮЛжУЙиЯЕЃЛ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌНЋЭМЃЈ1ЃЉжаЕФЁАACЁЭABЃЌBDЁЭABЁБЮЊИФЁАЁЯCABЃНЁЯDBAЃН60ЁуЁБЃЌЦфЫћЬѕМўВЛБфЃЎЩшЕу Q ЕФдЫЖЏЫйЖШЮЊ![]()
![]() ЃЌЪЧЗёДцдкЪЕЪ§
ЃЌЪЧЗёДцдкЪЕЪ§![]() ЃЌЪЙЕУЁїACP гыЁїBPQ ШЋЕШЃПШєДцдкЃЌЧѓГіЯргІЕФ
ЃЌЪЙЕУЁїACP гыЁїBPQ ШЋЕШЃПШєДцдкЃЌЧѓГіЯргІЕФ![]() ЁЂ
ЁЂ![]() ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввЁЂБћШ§ШЫеОГЩвЛКсХХееЯрЃЌвђМзЁЂввСНШЫЪЧКУгбЃЌееЯрЪБСНШЫНєСкзХеОдквЛЦ№ВЛЗжПЊЃЎ
ЃЈ1ЃЉЧыАДзѓЁЂжаЁЂгвЕФЫГађСаГіЫљгаЗћКЯвЊЧѓЕФеОЮЛЕФНсЙћЃЛ
ЃЈ2ЃЉАДвЊЧѓЫцЛњЕФеОСЂЃЌЧѓБћеОдкМззѓБпЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧгУЦхзгАкГЩЕФЁАІГЁБзжЭМАИЃЎДгЭМАИжаПЩвдПДГіЃЌЕк1ИіЁАІГЁБзжаЭЭМАИашвЊ5УЖЦхзгЃЎЕк2ИіЁАІГЁБзжаЭЭМАИашвЊ8УЖЦхзгЃЎЕк3ИіЁАІГЁБзжаЭЭМАИашвЊ11УЖЦхзгЃЌдђЕкnИіЁАІГЁБзжаЭЫљашЦхзгЕФИіЪ§ЃЈ ЃЉ

AЃЎ2n+3 BЃЎ3n+2 CЃЎ3n+4 DЃЎ3n+5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
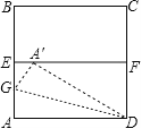
ЁОЬтФПЁПШчЭМЃЌABCDЪЧвЛеХБпГЄЮЊ4cmЕФе§ЗНаЮжНЦЌЃЌEЃЌFЗжБ№ЮЊABЃЌCDЕФжаЕуЃЌбиЙ§ЕуDЕФелКлНЋAНЧЗелЃЌЪЙЕУЕуAТфдкEFЩЯЕФЕуAЁфДІелКлНЛAEгкЕуGЃЌдђЁЯADG=____ЁуEG=___cm ЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com