解:(1)
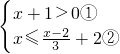
,
解①得x>-1,
解②得x≤2,
故不等式组的解集为-1<x≤2;
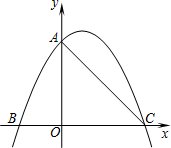
(2)∵△OAC为直角边长为6的等腰直角三角形,
∴A点坐标为(0,6),C点坐标为(6,0),
设二次函数的解析式为y=ax
2+bx+c(a、b、c为常数,a≠0),
则
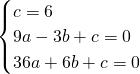
,
解得
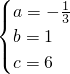
,
故抛物线的解析式为y=-

x
2+x+6.
分析:(1)分别解两个不等式得到x>-1和x≤2,然后根据大于小的小于大的取中间确定不等式组的解集;
(2)先确定A点坐标为(0,6),C点坐标为(6,0),然后利用待定系数法确定抛物线的解析式.
点评:本题考查了待定系数法求二次函数的解析式:先设二次函数的解析式为y=ax
2+bx+c(a、b、c为常数,a≠0),再把抛物线上三个点的坐标代入得到a、b、c的三元一次方程组,解方程组可确定二次函数的解析式.也考查了解不等式组.

 (1)解不等式组
(1)解不等式组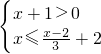
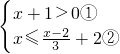 ,
,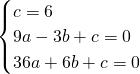 ,
,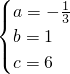 ,
, x2+x+6.
x2+x+6.
