
分析 连结OA、OB,如图,先根据切线的性质得∠PAO=∠PBO=90°,再根据四边形内角和计算出∠AOB=180°-∠APB=130°,然后分类讨论:当点C在优弧AB上,根据圆周角定理易得∠ACB=$\frac{1}{2}$∠AOB;当点C在劣弧AB上,即C′的位置,根据圆内接四边形的性质易得∠AC′B=180°-∠ACB,问题得解.
解答 解: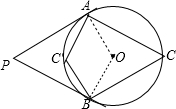 连结OA、OB,如图,
连结OA、OB,如图,
∵PA、PB分别切⊙O于A、B两点,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∴∠AOB=180°-∠APB=180°-50°=130°,
当点C在优弧AB上,则∠ACB=$\frac{1}{2}$∠AOB=65°;
当点C在劣弧AB上,即C′的位置,则∠AC′B=180°-∠ACB=180°-65°=115°,
即∠ACB为65°或115°.
故答案为65或115.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.也考查了圆周角定理和分类讨论思想的运用.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
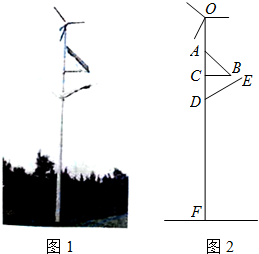 如图1,某利用风能、太阳能发电的风光互补环保路灯的灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,∠CDE=60°.且根据我市的地理位置设定太阳能板AB的倾斜角为43°,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍安全旋转,叶片与太阳能板顶端A的最近距离不少于0.5米,求灯杆OF至少要多高(利用科学计算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,结果保留两位小数)?
如图1,某利用风能、太阳能发电的风光互补环保路灯的灯杆顶端装有风力发电机,中间装有太阳能板,下端装有路灯.该系统工作过程中某一时刻的截面图如图2,已知太阳能板的支架BC垂直于灯杆OF,路灯顶端E距离地面6米,DE=1.8米,∠CDE=60°.且根据我市的地理位置设定太阳能板AB的倾斜角为43°,AB=1.5米,CD=1米.为保证长为1米的风力发电机叶片无障碍安全旋转,叶片与太阳能板顶端A的最近距离不少于0.5米,求灯杆OF至少要多高(利用科学计算器可求得sin43°≈0.6820,cos43°≈0.7314,tan43°≈0.9325,结果保留两位小数)?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
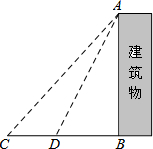 某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)
某中学九年级数学兴趣小组想测量建筑物AB的高度.他们在C处仰望建筑物顶端,测得仰角为48°,再往建筑物的方向前进6米到达D处,测得仰角为64°,求建筑物的高度.(测角器的高度忽略不计,结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com