
【题目】某超市十一优惠顾客,若一次性购物不超过300元不优惠,超过300元时按全额9折优惠.一位顾客第一次购物付款120元,第二次购物付款288元,若这两次购物合并成一次性付款可节省_____元.
【答案】40.8或12
【解析】
按照优惠条件第一次付120元时,所购买的物品价值不会超过300元,不享受优惠,因而第一次所购物品的价值就是120元;300元的9折是270元,因而第二次的付款288元所购买的商品价值可能超过300元,也有可能没有超过300元.计算出两次购买物品的价值的和,按优惠条件计算出应付款数.
(1)若第二次购物超过300元,
设此时所购物品价值为![]() 元,则90%
元,则90%![]() =288,解得:
=288,解得:![]() =320,
=320,
两次所购物价值为120+320=440>300,
所以享受9折优惠,因此应付440×90%=396(元).
这两次购物合并成一次性付款可节省:120+288-396=12(元).
(2)若第二次购物没有过300元,两次所购物价值为120+288=408(元),
因为408>300,
所以享受9折优惠,这两次购物合并成一次性付款可以节省:408×10%=40.8(元)
故答案为:40.8或12.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】下列两个三角形中,一定全等的是()
A. 两个等边三角形
B. 有一个角是![]() ,腰相等的两个等腰三角形
,腰相等的两个等腰三角形
C. 有一条边相等,有一个内角相等的两个等腰三角形
D. 有一个角是![]() ,底相等的两个等腰三角形
,底相等的两个等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,三角形△ABC为等腰直角三角形,AC=BC,BC交x轴于点D.
(1)若A(-4,0),C(0,2),求点B的坐标;
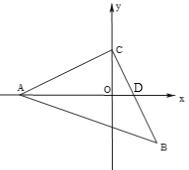
(2)若∠EDB=∠ADC,问∠ADE与∠CAD满足怎样的关系?并证明.
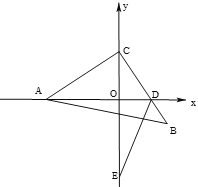
(3)若AD平分∠BAC,A(-4,0),D(m,0),B的纵坐标为n,试探究m、n之间满足怎样的关系?
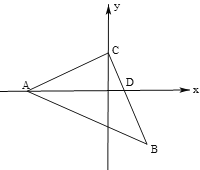
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市教委为了让广大青少年学生走向操场、走进自然、走到阳光下,积极参加体育锻炼,启动了“学生阳光体育运动”,其中有一项是短跑运动,短跑运动可以锻炼人的灵活性,增强人的爆发力,因此张明和李亮在课外活动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
成绩统计分析表
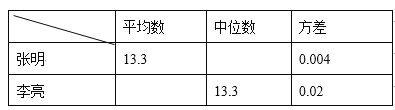
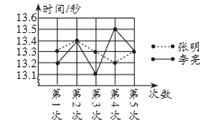
(1)张明第2次的成绩为__________秒;
(2)请补充完整上面的成绩统计分析表;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁? 请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
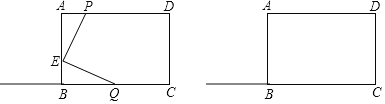
【题目】在长方形ABCD中,长方形ABCD的周长为36厘米,BC比AB大2厘米.点E在线段AB上,且AE=3BE,动点P从A点出发,在线段AD上以每秒1厘米的速度向终点D运动;动点Q从C点出发,沿着射线CB以每秒5厘米的速度运动,三角形APE的面积为S1,三角形EBQ的面积为S2,两点同时出发,当一个点停止运动时,另一个点也停止运动,设它们运动的时间为t秒.
(1)求AB、BC的长;
(2)请用含t的式子分别表示S1和S2;
(3)它们出发几秒时,S1=S2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)该二次函数图象的对称轴是x![]() ;
;
(2)若该二次函数的图象开口向下,当![]() 时,
时, ![]() 的最大值是2,求当
的最大值是2,求当![]() 时,
时, ![]() 的最小值;
的最小值;
(3)若对于该抛物线上的两点![]() ,
, ![]() ,当
,当![]() ,
, ![]() 时,均满足
时,均满足![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点A坐标为(2,0),点B在x轴负半轴上,C在y轴正半轴上,∠ACB=90°,∠ABC=30°.
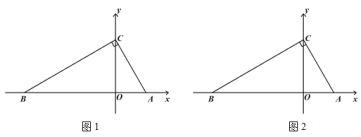
(1)求点B坐标;
(2)如图2,点P从B出发,沿线段BC运动,点P运动速度为每秒2个单位长度,设运动时间为t秒,用含t的式子表示三角形△OBP的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com