练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．计算：$\sqrt{32}$-cos45°+（1-$\sqrt{2}$）2．

    分析 直接化简二次根式结合完全平方公式计算得出答案．

    解答 解：$\sqrt{32}$-cos45°+（1-$\sqrt{2}$）2
    =4$\sqrt{2}$-$\frac{\sqrt{2}}{2}$+1+2-2$\sqrt{2}$
    =3+$\frac{3}{2}$$\sqrt{2}$．

    点评 此题主要考查了二次根式的混合运算，正确应用完全平方公式是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．如图，要从电线杆离地面4m处向地面拉一条钢索，若地面钢索固定点A到电线杆底部B的距离为2m，求钢索的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

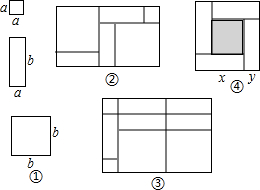    5．一天，王明和李玲玩纸片拼图游戏，发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式．比如图②可以解释为：（a+2b）（a+b）=a2+3ab+2b2．
    （1）图③可以解释为等式：（a+2b）（2a+b）=2a2+5ab+2b2
    （2）要拼出一个长为a+3b，宽为2a+b的长方形，需要如图①所示的2块，7块，3块．
    （3）如图④，大正方形的边长为m，小正方形的边长为n，若用x、y表示四个矩形的两边长（x＞y），观察图案，指出以下关系式：
    （1）xy=$\frac{{m}^{2}-{n}^{2}}{4}$（2）x+y=m（3）x2-y2=m•n（4）x2+y2=$\frac{{m}^{2}+{n}^{2}}{2}$
    其中正确的有D
    A．1个   B．2个    C．3个   D．4个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．某城市城区居民从2017年1月1日开始执行阶梯水价，收费标准如下表所示：
    平均月用水量不超过13.5立方米的部分超过13.5立方米不超过23立方米的部分超过23立方米的部分
    收费标准（元/立方米）3.84.657.18
    设该城市城区居民月用水量为x（立方米）时，每月应缴纳水费为y（元）．
    （1）求该城市城区居民每月应缴纳的水费y与月用水量x之间的函数关系式；
    （2）该城市城区居民小华家1月份缴纳水费为79.2元，则小华家1月份的用水量是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．（1）化简：（$\frac{1}{x+2}$-1）÷$\frac{1-{x}^{2}}{x+2}$
    （2）关于x的一元二次方程kx2+2x-3=0有两个不相等的实数根，求k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．方程x2-9x+18=0的两根是菱形ABCD两条对角线的长度，则该菱形的面积为9．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在平面直角坐标系中，经过的点A（-4，0）、点B（6，0）的 抛物线与y轴相交于点C（0，m），连接BC．
    （1）若△OAC∽△OCB，请求出m的值；
    （2）当m=3时，试求出抛物线的解析式；
    （3）在（2）的条件下，若P为抛物线上位于x轴上方的一动点，以P、A、B、C为顶点的四边形面积记作S，当S取何值时，相应的点P有且只有3个？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．（1）解方程组：$\left\{\begin{array}{l}{3x-2y=4}\\{x-2y=2}\end{array}\right.$
    （2）已知关于x的一元二次方程x2+2x-m=1有实数根，求m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．在平面直角坐标系中，点A（-3，2），B（3，5），C（x，y），若AC∥x轴，则线段BC的最小值及此时点C的坐标分别为（　　）
    A．6，（-3，5）B．10，（3，-5）C．1，（3，4）D．3，（3，2）

    查看答案和解析>>

    同步练习册答案