
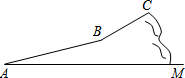
 今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔191米,C点海拔791米.
今年“五一”假期,某数学活动小组组织一次登山活动.他们从山脚下A点出发沿斜坡AB到达B点,再从B点沿斜坡BC到达山顶C点,路线如图所示.斜坡AB的长为1040米,斜坡BC的长为400米,在C点测得B点的俯角为30°,.已知A点海拔191米,C点海拔791米.分析 (1)过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,根据正弦的定义求出CD,计算得到B点的海拔;
(2)根据勾股定理求出AE,根据坡度的概念计算即可.
解答 解:(1)如图,过C作CF⊥AM,F为垂足,过B点作BE⊥AM,BD⊥CF,E、D为垂足.,
∵在C点测得B点的俯角为30°
∴∠CBD=30°,又BC=400米,
∴CD=400×sin30°=400×=200米.
∴B点的海拔为721-200=521米;
(2)∵BE=DF=521-121=400米,
又∵AB=1040米,
∴AE=$\sqrt{A{B}^{2}-B{E}^{2}}$=960米,
∴斜坡AB的坡度=400:960=1:2.4.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度的概念、熟记锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
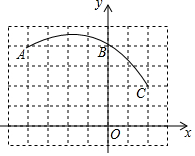 如图,在单位长度为1的正方形网格中建立平面直角坐标系,一段圆弧经过网格的交点为A(-4,4),B(0,4),C(2,2).
如图,在单位长度为1的正方形网格中建立平面直角坐标系,一段圆弧经过网格的交点为A(-4,4),B(0,4),C(2,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{34}{3}$ | B. | $\frac{10}{3}$ | C. | $\frac{34}{3}$ | D. | -$\frac{10}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点B、C、D都在半径为12的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为12的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com