

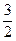
 ············································································ 2分
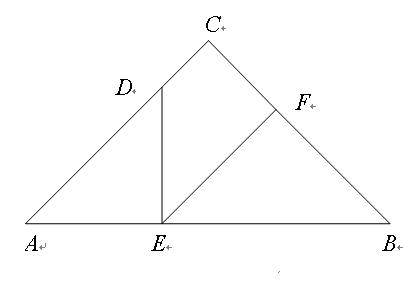
············································································ 2分 ,∴∠ADE+∠AED=135°;
,∴∠ADE+∠AED=135°;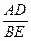 =
=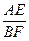 ,
,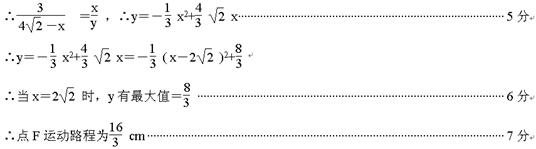
 ,
,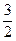
 s;
s;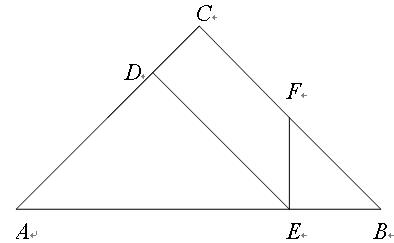
 ,
, s;
s;
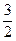
 s或3
s或3 s或3s.
s或3s.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源:不详 题型:解答题
 ,这个矩形的长宽各是多少?
,这个矩形的长宽各是多少?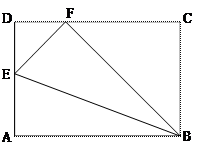
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
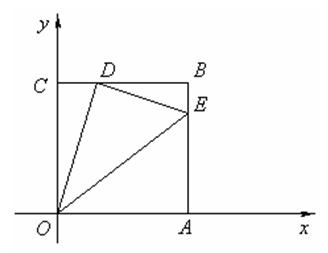
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
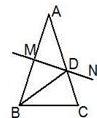
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 杆,利用太
杆,利用太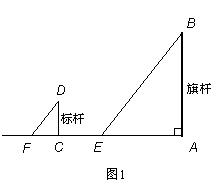
 出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离.
出必须的工具,设计一个测量方案,以求出旗杆顶端到地面的距离. 用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)
用图中画出示意图,说明需要测量的数据.(注意不能到达底部点N对完成测量任务的影响,不需计算)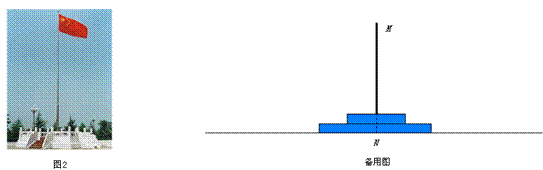
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
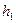 ,
,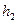 ,△OEF与△OGH组成的图形称为蝶形。
,△OEF与△OGH组成的图形称为蝶形。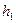 与
与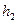 满足的关系式,并求
满足的关系式,并求 的取值范围。
的取值范围。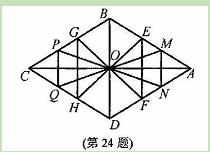
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
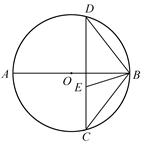
 3,CB="5" ,求DE的长.
3,CB="5" ,求DE的长.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 1)求证:△ABD为等腰三角形;
1)求证:△ABD为等腰三角形;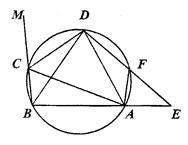
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com