Question

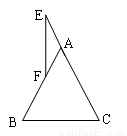
已知：如图所示，△ABC中，AB=AC，点E在CA的延长线上，且∠AEF=AFE，求证：EF⊥BC。

Answer 1

证明见解析.

【解析】

试题分析：延长EF交BC于点D，设∠AEF=∠AFE=∠BFD=x°，根据等腰三角形的性质及三角形外角的性质可得到∠B=∠C=90°-x°，再根据三角形内角和定理即可推出∠BDE=90°，从而得到EF和BC的位置关系为垂直．

试题解析：EF⊥BC．

延长EF交BC于点D，设∠AEF=∠AFE=∠BFD=x，

∵AB=AC，

∴∠B=∠C，

∵∠B+∠C=∠BAE=180°-2x，

∴∠B=∠C=90°-x，

∴∠BDE=180°-∠B-∠BFD=180°-（90°-x）-x=90°，

∴EF⊥BC．

考点：1.等腰三角形的性质；2.三角形内角和定理；3.三角形的外角性质．