解:(1)根据题意,得

,解得
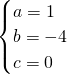
,
∴抛物线的解析式为y=x
2-4x;
(2)抛物线上存在一点P,使∠POM=90?.
x=-

=-

=2,y=

=
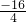
=-4,
∴顶点M的坐标为(2,-4),
设抛物线上存在一点P,满足OP⊥OM,其坐标为(a,a
2-4a),
过P点作PE⊥y轴,垂足为E;过M点作MF⊥y轴,垂足为F.
则∠POE+∠MOF=90?,∠POE+∠EPO=90?.
∴∠EPO=∠FOM.
∵∠OEP=∠MFO=90?,
∴Rt△OEP∽Rt△MFO.
∴OE:MF=EP:OF.
即(a
2-4a):2=a:4,
解得a
1=0(舍去),a
2=

,
∴P点的坐标为(

,

);
(3)过顶点M作MN⊥OM,交y轴于点N.则∠FMN+∠OMF=90?.
∵∠MOF+∠OMF=90?,
∴∠MOF=∠FMN.
又∵∠OFM=∠MFN=90?,
∴△OFM∽△MFN.
∴OF:MF=MF:FN. 即 4:2=2:FN.∴FN=1.
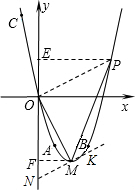
∴点N的坐标为(0,-5).
设过点M,N的直线的解析式为y=kx+b,则

,
解得
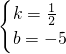
,∴直线的解析式为y=

x-5,
联立
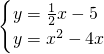
得x
2-

x+5=0,解得x
1=2,x
2=

,
∴直线MN与抛物线有两个交点(其中一点为顶点M).
另一个交点K的坐标为(

,-

),
∴抛物线上必存在一点K,使∠OMK=90?.坐标为(

,-

).
分析:(1)将A(1,-3),B(3,-3),C(-1,5)三点坐标代入y=ax
2+bx+c中,列方程组求a、b、c的值,得出抛物线解析式;
(2)抛物线上存在一点P,使∠POM=90?.设(a,a
2-4a),过P点作PE⊥y轴,垂足为E;过M点作MF⊥y轴,垂足为F,利用互余关系证明Rt△OEP∽Rt△MFO,利用相似比求a即可;
(3)抛物线上必存在一点K,使∠OMK=90?.过顶点M作MN⊥OM,交y轴于点N,在Rt△OMN中,利用互余关系证明△OFM∽△MFN,利用相似比求N点坐标,再求直线MN解析式,将直线MN解析式与抛物线解析式联立,可求K点坐标.
点评:本题考查了二次函数的综合运用.关键是通过已知三点求抛物线解析式,根据垂直关系证明三角形相似,得出线段长及点的坐标,利用直线解析式及抛物线解析式求满足条件的点的坐标.

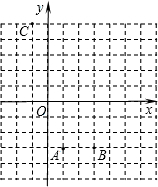 抛物线y=ax2+bx+c(a≠0)过点A(1,-3),B(3,-3),C(-1,5),顶点为M点.
抛物线y=ax2+bx+c(a≠0)过点A(1,-3),B(3,-3),C(-1,5),顶点为M点. ,解得
,解得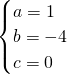 ,
, =-
=- =2,y=
=2,y= =
=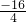 =-4,
=-4, ,
, ,
, );
);
 ,
,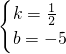 ,∴直线的解析式为y=
,∴直线的解析式为y= x-5,
x-5,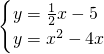 得x2-
得x2- x+5=0,解得x1=2,x2=
x+5=0,解得x1=2,x2= ,
, ,-
,- ),
), ,-
,- ).
).

 阅读快车系列答案
阅读快车系列答案

 (2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
(2012•陕西)如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.