
 如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( )
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠1=∠2;④△ACN≌△ABM.其中正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
|
|


科目:初中数学 来源: 题型:
 如图,有三条交叉的公路,现要在三条公路交叉所形成的区域内建一货运站,使得货运站到三条公路的路程一样长,请问如何确定货运站的位置?(保留作图痕迹) 简单叙述你的方法.
如图,有三条交叉的公路,现要在三条公路交叉所形成的区域内建一货运站,使得货运站到三条公路的路程一样长,请问如何确定货运站的位置?(保留作图痕迹) 简单叙述你的方法.查看答案和解析>>
科目:初中数学 来源: 题型:
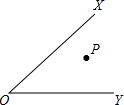 如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.写出你作图的主要步骤,并标明你所确定的点(要求画出草图,保留作图痕迹).
如图,∠XOY内有一点P,试在射线OX上找出一点M,在射线OY上找出一点N,使PM+MN+NP最短.写出你作图的主要步骤,并标明你所确定的点(要求画出草图,保留作图痕迹).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com