
如图,有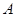 、
、 、
、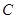 、
、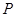 四个点,根据以下要求画图(保留画图痕迹)
四个点,根据以下要求画图(保留画图痕迹)
(1)画直线 ; (2)画线段
; (2)画线段 ; (3)画射线
; (3)画射线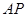 ;
;
(4)若点 在点
在点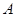 正东方向,那么点
正东方向,那么点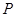 在点
在点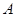 的 方向;
的 方向;
(5)在射线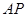 上取线段
上取线段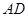 ,使
,使 (尺规作图);
(尺规作图);
(6)在平面上确定一点 ,使
,使 的长度最短,这是根据 原理.
的长度最短,这是根据 原理.
(1)(2)(3)(5)如图所示;(4)东偏南60°;(6)如图,两点之间线段最短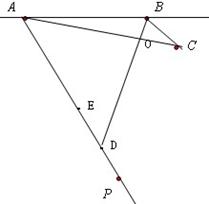
解析试题分析:(1)连接AB,并向两边无限延长即可得到结果;
(2)连接BC即可得到结果;
(3)连接AP,并向AP方向无限延长即可得到结果;
(4)先测量出∠BAD的度数,再根据方位角的定义即可得到结果;
(5)先在射线AP上截取AE=AB,再在射线EP上截取ED=BC,即可得到结果;
(6)连接AC、BD交于点O,则点O即为所求,其根据是:两点之间线段最短.
(1)(2)(3)(5)如图所示;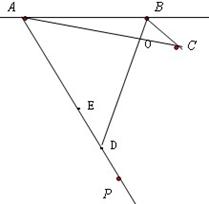
(4)若点 在点
在点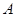 正东方向,那么点
正东方向,那么点 在点
在点 的东偏南60°;
的东偏南60°;
(6)如图所示,这是根据两点之间线段最短的原理.
考点:本题考查的是基本作图
点评:解答本题的关键是熟练掌握射线有一个端点,可以向一方无限延伸;直线没有端点,可以向两方无限延伸;线段有两个端点.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•普洱)如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,点Q的坐标记为Q(x,y).
(2013•普洱)如图,有A、B两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A转盘中指针指向的数字记为x,B转盘中指针指向的数字记为y,点Q的坐标记为Q(x,y).查看答案和解析>>
科目:初中数学 来源:2012-2013学年福建福州七年级上学期期末考试数学试卷(解析版) 题型:解答题
如图,有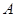 、
、 、
、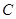 、
、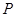 四个点,根据以下要求画图(保留画图痕迹)
四个点,根据以下要求画图(保留画图痕迹)
(1)画直线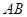 ; (2)画线段
; (2)画线段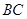 ; (3)画射线
; (3)画射线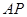 ;
;
(4)若点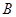 在点
在点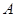 正东方向,那么点
正东方向,那么点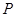 在点
在点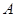 的 方向;
的 方向;
(5)在射线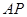 上取线段
上取线段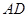 ,使
,使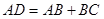 (尺规作图);
(尺规作图);
(6)在平面上确定一点 ,使
,使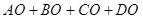 的长度最短,这是根据 原理.
的长度最短,这是根据 原理.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com