
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(3,0),其部分图象如图所示,下列结论:
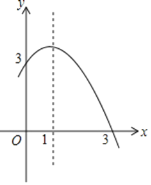
①4ac<b2;
②方程ax2+bx+c=0的两个根是x1=-2 x2=3;
③3a+c=0;
④当y>0时,x的取值范围是-1<x<3;
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )
A.4个B.3个C.2个D.1个
【答案】A
【解析】
利用抛物线与x轴的交点个数可对①进行判断;利用抛物线的对称性得到抛物线与x轴的一个交点坐标为(3,0),则可对②进行判断;由对称轴方程得到b=-2a,然后根据x=-1时函数值为0可得到3a+c=0,则可对③进行判断;根据抛物线在x轴上方所对应的自变量的范围可对④进行判断;根据二次函数的性质对⑤进行判断.
∵抛物线与x轴有2个交点,
∴b2-4ac>0,故①正确;
∵抛物线的对称轴为直线x=1,
而点(-1,0)关于直线x=1的对称点的坐标为(3,0),
∴方程ax2+bx+c=0的两个根是x1=-1,x2=3,故②错误;
∵x=-![]() =1,即b=-2a,
=1,即b=-2a,
而x=-1时,y=0,即a-b+c=0,
∴a+2a+c=0,故③正确;
∵抛物线与x轴的两点坐标为(-1,0),(3,0),
∴当-1<x<3时,y>0,故④正确;
∵抛物线的对称轴为直线x=1,
∴当x<1时,y随x增大而增大,故⑤正确.
综上所述,正确的结论有①③④⑤,共4个.
故选A.


科目:初中数学 来源: 题型:
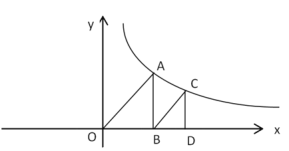
【题目】如下图,反比例函数![]() (
(![]() >0)图象上一点A,连结OA,作AB丄
>0)图象上一点A,连结OA,作AB丄![]() 轴于点B,作BC∥OA交反比例函数图象于点C,作CD丄
轴于点B,作BC∥OA交反比例函数图象于点C,作CD丄![]() 轴于点D,若点A、点C横坐标分别为m、n,则m:n的值为_______________.
轴于点D,若点A、点C横坐标分别为m、n,则m:n的值为_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
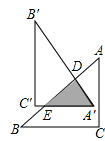
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.把△ABC绕AB边上的点D顺时针旋转90°得到△A′B′C′,A′C′交AB于点E.若AD=BE,则△A′DE的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年暑假,小丽爸爸的同事送给她爸爸一张北京故宫的门票,她和哥哥两人都很想去参观,可门票只有一张.读九年级的哥哥想了一个办法,他拿了八张扑克牌,将数字为1,2,3,5的四张牌给小丽,将数字为4,6,7,8的四张牌留给自己,并按如下游戏规则进行:小利哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌上的数字相加,如果和为偶数,和小丽去;如果和为奇数,则哥哥去.
(1)请用画树状图或列表的方法求小丽去北京故宫参观的概率;
(2)哥哥设计的游戏规则公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
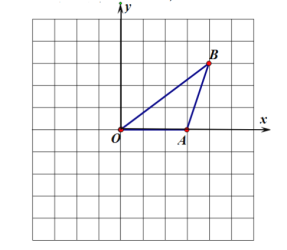
【题目】如图,在10×10的网格中,横、纵坐标均为整数的点叫做格点,例如A(3,0),B(4,3)都是格点。将△AOB绕点O顺时针旋转90°得到△COD(点A,B的对应点分别为点C 、D)。
(1)作出△COD,并写出下列各点的坐标:C( ),D( );
(2)仅用无刻度的直尺找一格点E,使得EB⊥AB,请标明格点E的位置;
(3)仅用无刻度的直尺在OB上找一点F,使得∠OAF=45°(请标明辅助格点M的位置)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课本中有一个例题:
有一个窗户形状如图1,上部是一个半圆,下部是一个矩形,如果制作窗框的材料总长为6m,如何设计这个窗户,使透光面积最大?
这个例题的答案是:当窗户半圆的半径约为0.35m时,透光面积最大值约为1.05m2.
我们如果改变这个窗户的形状,上部改为由两个正方形组成的矩形,如图2,材料总长仍为6m,利用图3,解答下列问题:

(1)若AB为1m,求此时窗户的透光面积?
(2)与课本中的例题比较,改变窗户形状后,窗户透光面积的最大值有没有变大?请通过计算说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2-4(k-1)x+4k2=0有两个实数根x1、x2
(1) 求k的取值范围
(2) 若x1x2-2|x1+x2|=4,求k的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用工件槽(如图1)可以检测一种铁球的大小是否符合要求,已知工件槽的两个底角均为90°,尺寸如图(单位:cm).将形状规则的铁球放入槽内时,若同时具有图1所示的A、B、E三个接触点,该球的大小就符合要求.图2是过球心O及A、B、E三点的截面示意图,求这种铁球的直径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com