
分析 (1)方程利用因式分解法求出解即可;
(2)方程利用公式法求出解即可;
(3)方程整理后,利用因式分解法求出解即可;
(4)方程利用两数的平方相等,两数相等或互为相反数求出解即可.
解答 解:(1)分解因式得:(x-2)(x+4)=0,
可得x-2=0或x+4=0,
解得:x=2或x=-4;
(2)这里a=2,b=4,c=-1,
∵△=16+8=24,
∴x=$\frac{-4±2\sqrt{6}}{4}$=$\frac{-2±\sqrt{6}}{2}$;
(3)方程整理得:x2+2x-15=0,
分解因式得:(x-3)(x+5)=0,
可得x-3=0或x+5=0,
解得:x=3或x=-5;
(4)开方得:x-1=2x+3或x-1=-2x-3,
解得:x=-4或x=-$\frac{2}{3}$.
点评 此题考查了解一元二次方程-因式分解法,公式法,以及直接开平方法,熟练掌握各种解法是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
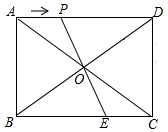 如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s.
如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
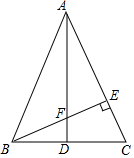 如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?
如图,△ABC中,AB=AC,AD是∠BAC的平分线,交BC于D,过点B作BE⊥AC于E,交AD于F,又知AF=2BD,△BCE与△AFE全等吗?为什么?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com