
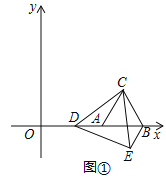
”¾ĢāÄæ”æČēĶ¼¢Ł£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µČ±ß”÷ABCµÄ¶„µćA£¬BµÄ×ų±ź·Ö±šĪŖ£Ø5£¬0£©£¬£Ø9£¬0£©£¬µćDŹĒxÖįÕż°ėÖįÉĻŅ»øö¶Æµć£¬Į¬½ÓCD£¬½«”÷ACDČʵćCÄꏱÕėŠż×Ŗ60”ćµĆµ½”÷BCE£¬Į¬½ÓDE£®
£Ø¢ń£©Ö±½ÓŠ“³öµćCµÄ×ų±ź£¬²¢ÅŠ¶Ļ”÷CDEµÄŠĪד£¬ĖµĆ÷ĄķÓÉ£»
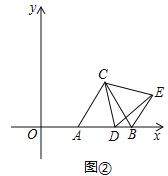
£Ø¢ņ£©ČēĶ¼¢Ś£¬µ±µćDŌŚĻ߶ĪABÉĻŌĖ¶ÆŹ±£¬”÷BDEµÄÖܳ¤ŹĒ·ń“ęŌŚ×īŠ”Öµ£æČō“ęŌŚ£¬Ēó³ö”÷BDEµÄ×īŠ”Öܳ¤¼°“ĖŹ±µćDµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£»
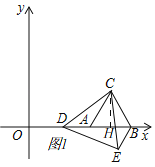
£Ø¢ó£©µ±”÷BDEŹĒÖ±½ĒČż½ĒŠĪŹ±£¬ĒóµćDµÄ×ų±ź£®£ØÖ±½ÓŠ“³ö½į¹ū¼“æÉ£©
”¾“š°ø”æ£Ø¢ń£©C![]() £¬”÷CDEŹĒµČ±ßČż½ĒŠĪ£»£Ø¢ņ£©“ęŌŚ£»
£¬”÷CDEŹĒµČ±ßČż½ĒŠĪ£»£Ø¢ņ£©“ęŌŚ£»![]() £»D£Ø7£¬0£©£»£Ø¢ó£©D£Ø1£¬0£©»ņ£Ø13£¬0£©£®
£»D£Ø7£¬0£©£»£Ø¢ó£©D£Ø1£¬0£©»ņ£Ø13£¬0£©£®
”¾½āĪö”æ·ÖĪö£ŗ
£Ø1£©ČēĶ¼1£¬¹żµćC×÷CH”ĶxÖįÓŚµćH£¬ÓÉ”÷ABCŹĒµČ±ßČż½ĒŠĪŅ×µĆAH=![]() AB=2£¬½įŗĻAC=AB=4”¢OA=5£¬æɵĆCH=
AB=2£¬½įŗĻAC=AB=4”¢OA=5£¬æɵĆCH=![]() £¬OH=7£¬ÓÉ“Ė¼“æɵƵ½µćCµÄ×ų±ź£»ÓÉŠż×ŖµÄŠŌÖŹæÉÖŖCE=CD£¬½įŗĻŠż×Ŗ½Ē”ĻDCE=60”ćæÉÖŖ”÷CDEŹĒµČ±ßČż½ĒŠĪ£»
£¬OH=7£¬ÓÉ“Ė¼“æɵƵ½µćCµÄ×ų±ź£»ÓÉŠż×ŖµÄŠŌÖŹæÉÖŖCE=CD£¬½įŗĻŠż×Ŗ½Ē”ĻDCE=60”ćæÉÖŖ”÷CDEŹĒµČ±ßČż½ĒŠĪ£»
£Ø2£©ČēĶ¼2£¬ÓÉ£Ø1£©æÉÖŖ”÷CDEŹĒµČ±ßČż½ĒŠĪ£¬ÓÉ“ĖæɵĆDE=CD£¬ÓÉ”÷CDEŹĒÓÉ”÷CADČʵćCŠż×ŖµĆµ½µÄ£¬ÓÉ“ĖæɵĆBE=AD£¬“Ó¶ųæɵƔ÷BDEµÄÖܳ¤=BD+BE+DE=BD+AD+CD=AB+CD=4+CD£¬ÓÉ“ĖæÉÖŖ£¬µ±CD”ĶABŹ±£¬CD×īŠ”£¬“ĖŹ±”÷BDEµÄÖܳ¤×īŠ”£¬ÓÉ£Ø1£©æÉÖŖ£¬“ĖŹ±CD=![]() £¬OD=7£¬¼“µ±µćDµÄ×ų±źĪŖ£Ø7£¬0£©Ź±£¬”÷BDEµÄÖܳ¤×īŠ”£¬×īŠ”ÖµĪŖ
£¬OD=7£¬¼“µ±µćDµÄ×ų±źĪŖ£Ø7£¬0£©Ź±£¬”÷BDEµÄÖܳ¤×īŠ”£¬×īŠ”ÖµĪŖ![]() £»
£»
£Ø3£©ČēĶ¼3£¬ÓÉ”ĻCBE=”ĻCAD=120”ćæɵƔĻABC=60”ć£¬ÓÉ“ĖæɵƔĻDBE=60”攣90”ć£¬½įŗĻ”÷BDEŹĒÖ±½ĒČż½ĒŠĪ£¬æÉÖŖ£ŗ“ęŌŚ¢Ł”ĻBED=90”ć£»¢Ś”ĻBDE=90”ć£ØČēĶ¼3£¬”ĻBD'E'=90”ć£©Į½ÖÖĒéæö£¬·ÖĮ½ÖÖĒéæö»³ö·ūŗĻŅŖĒóµÄĶ¼ŠĪ£¬²¢½įŗĻŅŃÖŖĢõ¼ž½ųŠŠ·ÖĪö¼ĘĖć¼“æÉ.
Ļź½ā£ŗ
£Ø¢ń£©ČēĶ¼1£¬¹żµćC×÷CH”ĶABÓŚH£¬
”ß”÷ABCŹĒµČ±ßČż½ĒŠĪ£¬CH”ĶABÓŚµćH£¬
”ą”ĻAHC=90”ć£¬AH=![]() AB=
AB=![]() £Ø9©5£©=2£¬
£Ø9©5£©=2£¬
”ąOH=OA+AH=7£¬
”ßAC=AB=4£¬
”ąŌŚRt”÷ACHÖŠ£¬CH=![]() £¬
£¬
”ą C![]() £»
£»
”ß”÷CBEŹĒÓÉ”÷CADČʵćCÄꏱÕėŠż×Ŗ60”ćµĆµ½µÄ£¬
”ą”ĻDCE=60”ć£¬DC=EC£¬
”ą”÷CDEŹĒµČ±ßČż½ĒŠĪ£»
£Ø¢ņ£©“ęŌŚ£¬ĄķÓÉČēĻĀ£ŗČēĶ¼2£¬Óɣآń£©ÖŖ£¬”÷CDEŹĒµČ±ßČż½ĒŠĪ£¬
”ąDE=CD£¬
ÓÉŠż×ŖÖŖ£¬BE=AD£¬
”ąC”÷DBE=BE+DB+DE=AB+DE=4+DE=4+CD£¬
ÓÉ“¹Ļ߶Ī×ī¶ĢæÉÖŖ£¬CD”ĶABÓŚDŹ±£¬”÷BDEµÄÖܳ¤×īŠ”£¬“ĖŹ±£¬ÓÉ£Ø1£©æÉÖŖCD=2![]() £¬OD=7£¬
£¬OD=7£¬
”ą”÷BDEµÄÖܳ¤×īŠ”ÖµĪŖ4+2![]() £¬µćD£Ø7£¬0£©£»
£¬µćD£Ø7£¬0£©£»
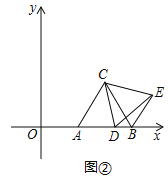
£Ø¢ó£©ČēĶ¼3£¬
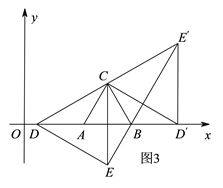
”ßÓÉŠż×ŖÖŖ£¬”ĻCBE=”ĻCAD=120”ć£¬
”ß”ĻABC=60”ć£¬
”ą”ĻDBE=60”攣90”ć£¬
”ß”÷BDEŹĒÖ±½ĒČż½ĒŠĪ£¬
”ą“ęŌŚ”ĻBED=90”ć»ņ”ĻBDE=90”ć£ØČēĶ¼3£¬”ĻBD'E'=90”ć£©Į½ÖÖĒéæö£¬
¢Łµ±”ĻBED=90”揱£¬
”ß”÷CDEŹĒµČ±ßČż½ĒŠĪ£¬
”ą”ĻCED=60”ć£¬
”ą”ĻBEC=30”ć£¬
”ß”ĻCBE=”ĻCAD=120”ć£¬
”ą”ĻBCE=30”ć£¬
”ąBE=BC=AB=4£¬
ŌŚRt”÷BDEÖŠ£¬”ĻDBE=”ĻCBE©”ĻABC=60”ć£¬
”ąBD=2BE=8£¬
”ßOB=9£¬
”ąOD=OB©BD=1£¬
”ąD£Ø1£¬0£©£¬
¢Śµ±”ĻBD'E'=90”揱£¬
”ß”÷CD'E'ŹĒµČ±ßČż½ĒŠĪ£¬
”ą”ĻCD'E'=60”ć£¬
”ą”ĻBD'C=30”ć£¬
”ß”ĻABC=60”ć£¬
”ą”ĻBCD'=30”ć=”ĻBD'E£¬
”ąBD'=BC=6£¬
”ßOB=9£¬
”ąOD'=OB+BD'=13£¬
”ąD'£Ø13£¬0£©£¬
¼“£ŗ“ęŌŚµćDŹ¹”÷BDEŹĒÖ±½ĒČż½ĒŠĪ£¬“ĖŹ±µćDµÄ×ų±ź·Ö±šĪŖ£ŗ£Ø1£¬0£©»ņ£Ø13£¬0£©£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
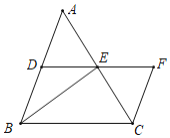
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬µćD£¬E·Ö±šŹĒ±ßAB£¬ACµÄÖŠµć£¬¹żµćC×÷CF”ĪAB½»DEµÄŃÓ³¤ĻßÓŚµćF£¬Į¬½ÓBE£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪBCFDŹĒĘ½ŠŠĖıߊĪ£®
£Ø2£©µ±AB=BCŹ±£¬ČōBD=2£¬BE=3£¬ĒóACµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŅŃÖŖÖ±Ļß![]() Óė
Óė![]() Öį”¢
Öį”¢![]() Öį·Ö±š½»ÓŚ
Öį·Ö±š½»ÓŚ![]() ”¢
”¢![]() Į½µć£¬µć
Į½µć£¬µć![]() ŹĒ
ŹĒ![]() ÖįÉĻŅ»¶Æµć£¬ŅŖŹ¹µć
ÖįÉĻŅ»¶Æµć£¬ŅŖŹ¹µć![]() ¹ŲÓŚÖ±Ļß
¹ŲÓŚÖ±Ļß![]() µÄ¶Ō³ĘµćøÕŗĆĀäŌŚ
µÄ¶Ō³ĘµćøÕŗĆĀäŌŚ![]() ÖįÉĻ£¬Ōņ“ĖŹ±µć
ÖįÉĻ£¬Ōņ“ĖŹ±µć![]() µÄ×ų±źŹĒ£Ø £©
µÄ×ų±źŹĒ£Ø £©
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ö±ĻßAB£ŗy=kx+4£Øk”Ł0£©ÓėxÖį£¬yÖį£¬½»ÓŚA”¢BĮ½µć£¬µćCŹĒBOµÄÖŠµćĒŅtan”ĻABO=![]()
£Ø1£©ĒóÖ±ĻßACµÄ½āĪöŹ½£»
£Ø2£©ČōµćMŹĒÖ±ĻßACµÄŅ»µć£¬µ±![]() Ź±£¬ĒóµćMµÄ×ų±ź.
Ź±£¬ĒóµćMµÄ×ų±ź.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
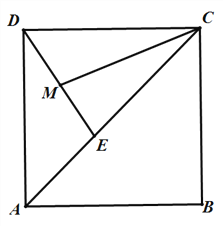
”¾ĢāÄæ”æŌŚĮāŠĪABCDÖŠ£¬ACŹĒ¶Ō½ĒĻߣ¬CD=CE£¬Į¬½ÓDE£¬µćMŹĒĻ߶ĪDEµÄÖŠµć.
£Ø1£©ČēĶ¼1£¬Į¬½ÓCM£¬ČōAC=16£¬CD=10£¬ĒóDEµÄ³¤
£Ø2£©ČēĶ¼2£¬µćFŌŚĮāŠĪµÄĶā²æ£¬DF=DM£¬ĒŅ”ĻCDA=”ĻFDE£¬Į¬½ÓFM½»ADÓŚµćG£¬FMµÄŃÓ³¤Ļß½»ACÓŚµćN£¬ĒóÖ¤£ŗCN=AG.
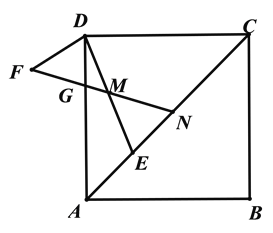
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖab£¼0£¬![]() £¬ĒŅ|c|£¾|b|£¾|a|£¬ŹżÖįÉĻa”¢b”¢c¶ŌÓ¦µÄµćŹĒA”¢B”¢C.
£¬ĒŅ|c|£¾|b|£¾|a|£¬ŹżÖįÉĻa”¢b”¢c¶ŌÓ¦µÄµćŹĒA”¢B”¢C.
(1) Čō|a|£½£aŹ±£¬ĒėŌŚŹżÖįÉĻ±ź³öA”¢B”¢CµÄ“óÖĀĪ»ÖĆ£»
(2) ŌŚ(1)µÄĢõ¼žĻĀ£¬»Æ¼ņ£ŗ|a£b|£|b£«c|£«|c£«a|.
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ŌČĪŅāŅ»øöČżĪ»Źż![]() £¬Čē¹ū
£¬Čē¹ū![]() Āś×ćø÷øöŹżĪ»ÉĻµÄŹż×Ö»„²»ĻąĶ¬£¬ĒŅ¶¼²»ĪŖĮć£¬ÄĒĆ“³ĘÕāøöŹżĪŖ”°ĻąŅģŹż”±£¬½«Ņ»øö”°ĻąŅģŹż”±ČĪŅāĮ½øöŹżĪ»ÉĻµÄŹż×Ö¶Ōµ÷ŗóæÉŅŌµĆµ½Čżøö²»Ķ¬µÄŠĀČżĪ»Źż£¬°ŃÕāČżøöŠĀČżĪ»ŹżµÄŗĶÓė111µÄÉĢ¼ĒĪŖ
Āś×ćø÷øöŹżĪ»ÉĻµÄŹż×Ö»„²»ĻąĶ¬£¬ĒŅ¶¼²»ĪŖĮć£¬ÄĒĆ“³ĘÕāøöŹżĪŖ”°ĻąŅģŹż”±£¬½«Ņ»øö”°ĻąŅģŹż”±ČĪŅāĮ½øöŹżĪ»ÉĻµÄŹż×Ö¶Ōµ÷ŗóæÉŅŌµĆµ½Čżøö²»Ķ¬µÄŠĀČżĪ»Źż£¬°ŃÕāČżøöŠĀČżĪ»ŹżµÄŗĶÓė111µÄÉĢ¼ĒĪŖ![]() .ĄżČē
.ĄżČē![]() £¬¶Ōµ÷°ŁĪ»ÓėŹ®Ī»ÉĻµÄŹż×ֵƵ½213£¬¶Ōµ÷°ŁĪ»ÓėøöĪ»ÉĻµÄŹż×ֵƵ½321£¬¶Ōµ÷Ź®Ī»ÓėøöĪ»ÉĻµÄŹż×ֵƵ½132£¬ÕāČżøöŠĀČżĪ»ŹżµÄŗĶĪŖ213+321+132=666£¬666”Ā111=6£¬ĖłŅŌ
£¬¶Ōµ÷°ŁĪ»ÓėŹ®Ī»ÉĻµÄŹż×ֵƵ½213£¬¶Ōµ÷°ŁĪ»ÓėøöĪ»ÉĻµÄŹż×ֵƵ½321£¬¶Ōµ÷Ź®Ī»ÓėøöĪ»ÉĻµÄŹż×ֵƵ½132£¬ÕāČżøöŠĀČżĪ»ŹżµÄŗĶĪŖ213+321+132=666£¬666”Ā111=6£¬ĖłŅŌ![]() .
.
£Ø1£©¼ĘĖć£ŗ![]() ŗĶ
ŗĶ![]() £»
£»
£Ø2£©Čō![]() ŹĒ”°ĻąŅģŹż”±£¬Ö¤Ć÷£ŗ
ŹĒ”°ĻąŅģŹż”±£¬Ö¤Ć÷£ŗ![]() µČÓŚ
µČÓŚ![]() µÄø÷ŹżĪ»ÉĻµÄŹż×ÖÖ®ŗĶ.
µÄø÷ŹżĪ»ÉĻµÄŹż×ÖÖ®ŗĶ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ŠŠĖıߊĪABCDÖŠ£¬µćE£¬FŌŚ¶Ō½ĒĻßACÉĻ£¬ĒŅAE=CF”£
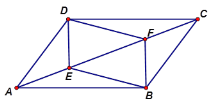
£Ø1£©ĒóÖ¤£ŗĖıߊĪDEBFŹĒĘ½ŠŠĖıߊĪ£»
£Ø2£©ČōDE=3£¬CD=4£¬”ĻEDC=90”ć£¬µ±ĖıߊĪDEBFŹĒĮāŠĪŹ±£¬AEµÄ³¤ĪŖ¶ąÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
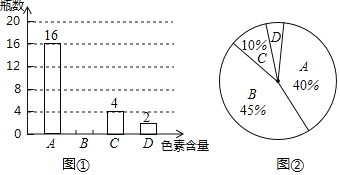
”¾ĢāÄæ”æŹ³Ę·°²Č«¹ŲĻµµ½ĪŅĆĒĆæøöČĖµÄÉķŠÄ½”æµ£¬ĪŖĮĖµ÷²éŹŠ³”ÉĻÄ³Ę·ÅĘŅūĮĻµÄÉ«ĖŲŗ¬ĮæŹĒ·ń·ūŗĻ¹ś¼Ņ±ź×¼£¬¹¤×÷ČĖŌ±ŌŚ³¬ŹŠĄļĖ껜³éČ”ĮĖøĆĘ·ÅĘŅūĮĻ½ųŠŠ¼ģŃ飬Ķ¼¢ŁŗĶĶ¼¢ŚŹĒøł¾Żµ÷²é½į¹ū»ęÖʵÄĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬ĘäÖŠA”¢B”¢C”¢D·Ö±š“ś±ķÉ«ĖŲŗ¬ĮæĪŖ0.05%ŅŌĻĀ”¢0.05%”«0.1%”¢0.1%”«0.15%”¢0.15%ŅŌÉĻ£¬Ķ¼¢ŁµÄĢõŠĪĶ³¼ĘĶ¼±ķŹ¾µÄŹĒ³é²éµÄŅūĮĻÖŠø÷ÖÖÉ«ĖŲŗ¬Įæ·Ö²¼µÄĘæŹż£¬Ķ¼¢ŚµÄÉČŠĪĶ³¼ĘĶ¼±ķŹ¾µÄŹĒ³é²éµÄŅūĮĻÖŠø÷ÖÖÉ«ĖŲŗ¬ĮæµÄĘæŹżÕ¼³é²é×ÜŹżµÄ°Ł·Ö±Č£®
Ēėøł¾ŻŅŌÉĻŠÅĻ¢½ā“šŅŌĻĀĪŹĢā£ŗ
£Ø1£©±¾“Īµ÷²éŅ»¹²³é²éĮĖ¶ąÉŁĘæŅūĮĻ£æ
£Ø2£©Ēė½«Ķ¼¢ŁĢõŠĪĶ³¼ĘĶ¼ÖŠÉ«ĖŲŗ¬ĮæĪŖBµÄ²æ·Ö²¹³äĶźÕū£»
£Ø3£©Ķ¼¢ŚÉČŠĪĶ³¼ĘĶ¼ÖŠÉ«ĖŲŗ¬ĮæĪŖDµÄ²æ·ÖµÄÉČŠĪŌ²ŠÄ½ĒŹĒ¶ąÉŁ¶Č£æ
£Ø4£©ČōÉ«ĖŲŗ¬Į泬¹ż0.15%¼“ĪŖ²»ŗĻøń²śĘ·£¬Ä³³¬ŹŠÕāÖÖĘ·ÅʵÄŅūĮĻ¹²ÓŠ5000Ę棬¹Ą¼ĘĘäÖŠ²»ŗĻøńµÄ²śĘ·Ō¼ÓŠ¶ąÉŁĘæ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com