练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】下列说法正确的是（ ）
    A.π一定是正数
    B.﹣a一定是负数
    C.+a一定是正数
    D.3+a一定是正数

    【答案】A
    【解析】解：∵a为任意数，∴﹣a，+a，3+a的正负性没法判断，而π是常数，是正数； 故选A．
    【考点精析】本题主要考查了正数与负数的相关知识点，需要掌握大于0的数叫正数；小于0的数叫负数；0既不是正数也不是负数；正数负数表示具有相反意义的量才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直径坐标系中，反比例函数y＝（x＞0）的图象上有一点A（m，4），过点A作AB⊥x轴于点B，将点B向右平移2个单位长度得到点C，过点C作y轴的平行线交反比例函数的图象于点D，CD＝．

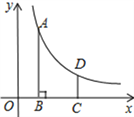
    （1）求点D的横坐标（用含m的式子表示）；

    （2）求反比例函数的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：
    （1）（﹣3a2b3）2（﹣a3b2）5÷a2b4；
    （2）（ ）2012×（﹣1.5）2013÷（﹣1）2014；
    （3）[x（x2y2﹣xy）﹣y（x2﹣x3y）]÷3x2y；
    （4）（5x+7y﹣3）（5x﹣7y+3）；
    （5）（a+2b﹣c）2；
    （6）（x+2y）2（x﹣2y）2 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算a3a2正确的是（　　）
    A.a
    B.a5
    C.a6
    D.a9

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道，如果两个三角形全等，则它们面积相等，而两个不全等的三角形，在某些情况下，可通过证明等底等高来说明它们的面积相等．已知△ABC与△DEC是等腰直角三角形，∠ACB=∠DCE=90°，连接AD、BE．

    （1）如图1，当∠BCE=90°时，求证：S△ACD=S△BCE；
    （2）如图2，当0°＜∠BCE＜90°时，上述结论是否仍然成立？如果成立，请证明；如果不成立，说明理由．
    （3）如图3，在（2）的基础上，作CF⊥BE，延长FC交AD于点G，求证：点G为AD中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC三个定点坐标分别为A（﹣1，3），B（﹣1，1），C（﹣3，2）．

    （1）请画出△ABC关于y轴对称的△A1B1C1；

    （2）以原点O为位似中心，将△A1B1C1放大为原来的2倍，得到△A2B2C2，请在第三象限内画出△A2B2C2，并求出S△A1B1C1：S△A2B2C2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=(x－4)(x＋2)的对称轴方程为（ ）

    A.直线x=-2B.直线x=1C.直线x=-4D.直线x=4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某汽车经销商购进两种型号的低排量汽车，其中型汽车的进货单价比型汽车的进货单价多2万元，经销商花50万元购进型汽车的数量与花40万元购进型汽车的数量相等．销售中发现型汽车的每周销量（台）与售价（万元/台）满足函数关系式， 型汽车的每周销量（台）与售价（万元/台）满足函数关系式．

    （1）求两种型号的汽车的进货单价；

    （2）已知型汽车的售价比型汽车的售价高2万元/台，设型汽车售价为万元/台．每周销售这两种车的总利润为万元，求与的函数关系式， 两种型号的汽车售价各为多少时，每周销售这两种车的总利润最大？最大总利润是多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】解下列方程：

    (1) ；

    (2) .

    查看答案和解析>>

    同步练习册答案