
【题目】综合题
(1)【阅读发现】如图①,在△ABC中,∠ACB=45°,AD⊥BC于点D,E为AD上一点,且DE=BD,可知AB=CE.
(2)【类比探究】如图②,在正方形ABCD中,对角线AC与BD交于点O,E是OC上任意一点,AG⊥BE于点G,交BD于点F.判断AF与BE的数量关系,并加以证明.
(3)【推广应用】在图②中,若AB=4,BF= ![]() ,则△AGE的面积为 .
,则△AGE的面积为 . 
【答案】
(1)
解:∵AD⊥BC,∠ACB=45°,
∴∠ADB=∠CDE=90°,△ACD是等腰直角三角形,
∴AD=CD,
在△ABD和△CED中, 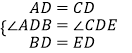 ,
,
∴△ABD≌△CED(SAS),
∴AB=CE;
(2)
解:AF=BE;理由如下:
∵正方形ABCD中,AB=BC=AD,∠BAD=90°,∠ABF=∠BCE=45°,AC⊥BD,OA=OB=OC,
∵AG⊥BE,
∴∠FAD+∠AFO=90°,
∵AG⊥BE,
∴∠FAO+∠AEG=90°,
∴∠AFO=∠AEG,
∵∠AFB=∠FAO+90°,
∴∠AFB=∠BEC,
在△ABF和△BCE中, 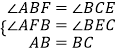 ,
,
∴△ABF≌△BCE(AAS),
∴AF=BE;
(3)![]()
【解析】【推广应用】解:∵AB=AD=4,∠BAD=90°,
∴BD= ![]() =4
=4 ![]() ,
,
∴OA=OB=OC= ![]() BD=2
BD=2 ![]() ,
,
∵BF= ![]() ,
,
∴OF=OB﹣BF= ![]() ,
,
∴AF= ![]() =
= ![]() ,
,
由角的互余性质得:∠OAF=∠OBE,
在△OBE和△OAF中, 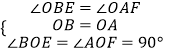 ,
,
∴△OBE≌△OAF(ASA),
∴OE=OE= ![]() ,
,
∴AE=OA+OE=3 ![]() ,
,
∵∠OAF=∠GAE,∠AOF=∠AGE=90°,
∴△AOF∽△AGE,
∴ ![]() ,即
,即 ![]() ,
,
解得:GE= ![]() ,AG=
,AG= ![]() ,
,
∴△AGE的面积= ![]() AGGE=
AGGE= ![]() ×
× ![]() ×
× ![]() =
= ![]() ;
;
所以答案是: ![]() .
.
【考点精析】掌握等腰直角三角形和勾股定理的概念是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】某农户承包种植某水果,今年投资30 000元,收获水果20 000千克.此水果在市场上的售价为每千克![]() 元,卖给到果园收购的商贩每千克
元,卖给到果园收购的商贩每千克![]() 元(
元(![]() .若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.
.若农户将水果拉到市场上出售,则平均每天可售1000千克,需雇佣2人,每人每天付工资150元,运输及其他税费平均每天200元.
(1)分别用含![]() 的代数式表示两种出售方式的纯收入.
的代数式表示两种出售方式的纯收入.
(2)若![]() ,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.
,且两种出售方式在相同的时间内售完全部水果.请通过计算说明哪种出售方式较好.
(3)该农户总结今年的种植及销售的经验,加强果园管理,力争明年纯收入达到100000元,则与(2)中今年较好的出售方式的纯收入相比,明年的纯收入的增长率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复习“全等三角形”的知识时,老师布置了一道作业题:
“如图①,已知,在△ABC中,AB=AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连接BQ,CP,则BQ=CP.”
小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ=CP之后,他将点P移到等腰三角形ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图②给出证明.
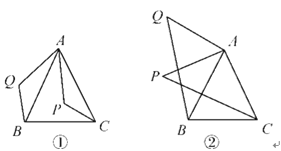
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=2,BC边上有10个不同的点P1,P2,……,P10, 记![]() (i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
(i = 1,2,……,10),那么 M1+M2+……+M10的值为( )
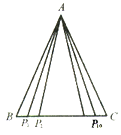
A. 4 B. 14 C. 40 D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=9,AB=15,动点P从点A出发,沿AC→CB→BA边运动,点P在AC、CB、BA边上运动的速度分别为每秒3、4、5个单位,直线l从与AC重合的位置开始,以每秒 ![]() 个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
(1)当t=秒时,△PCE是等腰直角三角形;
(2)当点P在AC边上运动时,将△PEF绕点E逆时针旋转,使得点P的对应点P1落在EF上,点F的对应点为F1 , 当EF1⊥AB时,求t的值;
(3)作点P关于直线EF的对称点Q,在运动过程中,若形成的四边形PEQF为菱形,求t的值;
(4)在整个运动过程中,设△PEF的面积为S,请直接写出S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量出大楼AB的高度,从距离楼底B处50米的点C(点C与楼底B在同一水平面上)出发,沿倾斜角为30°的斜坡CD前进20米到达点D,在点D处测得楼顶A的仰角为64°,求大楼AB的高度(结果精确到1米)(参考数据:sin64°≈0.9,cos64°≈0.4,tan64°≈2.1, ![]() ≈1.7)
≈1.7)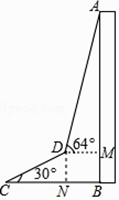
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,点M,N把线段AB分割成AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
请解决下列问题:
(1)已知点M,N是线段AB的勾股分割点,且BN>MN>AM.若AM=2,MN=3,求BN的长;
(2)如图2,若点F、M、N、G分别是AB、AD、AE、AC边上的中点,点D,E是线段BC的勾股分割点,且EC>DE>BD,求证:点M,N是线段FG的勾股分割点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲进行了10次射击训练,平均成绩为9环,且前9次的成绩(单位:环)依次为:8,10,9,10,7,9,10,8,10.
(1)求甲第10次的射击成绩;
(2)求甲这10次射击成绩的方差;
(3)乙在相同情况下也进行了10次射击训练,平均成绩为9环,方差为1.6环2,请问甲和乙哪个的射击成绩更稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
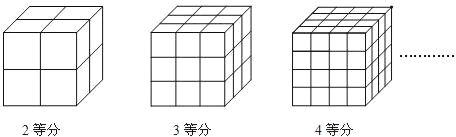
【题目】将一个正方体的表面全涂上颜色.
(1)如果把正方体的棱2等分,然后沿等分线把正方体切开,能够得到8个小正方体,设其中3面被涂上颜色的有a个,则a= ;
(2)如果把正方体的棱三等分,然后沿等分线把正方体切开,能够得到27个小正方体.设这些小正方体中有3个面涂有颜色的有a个,各个面都没有涂色的有b个,则a+b= ;
(3)如果把正方体的棱4等分,然后沿等分线把正方体切开,能够得到64个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= ;
(4)如果把正方体的棱n等分,然后沿等分线把正方体切开,能够得到 个小正方体.设这些小正方体中有2个面涂有颜色的有c个,各个面都没有涂色的有b个,则c+b= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com