Question

5．已知如图1，抛物线y=-$\frac{3}{8}$x²-$\frac{3}{4}$x+3与x轴交于A和B两点（点A在点B的左侧），与y轴相交于点C，点D的坐标是（0，-1），连接BC、AC

（1）求出直线AD的解析式；
（2）如图2，若在直线AC上方的抛物线上有一点F，当△ADF的面积最大时，有一线段MN=$\sqrt{5}$（点M在点N的左侧）在直线BD上移动，首尾顺次连接点A、M、N、F构成四边形AMNF，请求出四边形AMNF的周长最小时点N的横坐标；
（3）如图3，将△DBC绕点D逆时针旋转α°（0＜α°＜180°），记旋转中的△DBC为△DB′C′，若直线B′C′与直线AC交于点P，直线B′C′与直线DC交于点Q，当△CPQ是等腰三角形时，求CP的值．

Answer 1

分析 （1）先求出点A，B坐标，再用待定系数法求出直线AD解析式；
（2）先建立S_△ADF=-$\frac{3}{4}$（m+$\frac{2}{3}$）²+$\frac{25}{3}$，进而求出F点的坐标，再确定出点M的位置，进而求出点A₁，A₂坐标，即可确定出A₂F的解析式为y=-$\frac{107}{16}$x-$\frac{9}{8}$①，和直线BD解析式为y=-$\frac{1}{2}$x-1②，联立方程组即可确定出结论；
（3）分四种情况讨论计算，利用锐角三角函数和勾股定理表示出线段，用相似三角形的性质即可求出PC的值．

解答 解：（1）∵抛物线y=-$\frac{3}{8}$x²-$\frac{3}{4}$x+3与x轴交于A和B两点，
∴0=-$\frac{3}{8}$x²-$\frac{3}{4}$x+3，
∴x=2或x=-4，
∴A（-4，0），B（2，0），
∵D（0，-1），
∴直线AD解析式为y=-$\frac{1}{4}$x-1；

（2）如图1，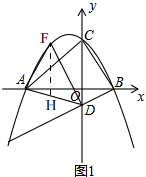
过点F作FH⊥x轴，交AD于H，
设F（m，-$\frac{3}{8}$m²-$\frac{3}{4}$m+3），H（m，-$\frac{1}{4}$m-1），
∴FH=-$\frac{3}{8}$m²-$\frac{3}{4}$m+3-（-$\frac{1}{4}$m-1）=-$\frac{3}{8}$m²-$\frac{1}{2}$m+4，
∴S_△ADF=S_△AFH+S_△DFH=$\frac{1}{2}$FH×|y_D-y_A|=2FH=2（-$\frac{3}{8}$m²-$\frac{1}{2}$m+4）=-$\frac{3}{4}$m²-m+8=-$\frac{3}{4}$（m+$\frac{2}{3}$）²+$\frac{25}{3}$，
当m=-$\frac{2}{3}$时，S_△ADF最大，
∴F（-$\frac{2}{3}$，$\frac{10}{3}$）
如图2，
作点A关于直线BD的对称点A₁，把A₁沿平行直线BD方向平移到A₂，且A₁A₂=$\sqrt{5}$，
连接A₂F，交直线BD于点N，把点N沿直线BD向左平移$\sqrt{5}$得点M，此时四边形AMNF的周长最小．
∵OB=2，OD=1，
∴tan∠OBD=$\frac{1}{2}$，
∵AB=6，
∴AK=$\frac{6\sqrt{5}}{5}$，
∴AA₁=2AK=$\frac{12\sqrt{5}}{5}$，
在Rt△ABK中，AH=$\frac{12}{5}$，A₁H=$\frac{24}{5}$，
∴OH=OA-AH=$\frac{8}{5}$，
∴A₁（-$\frac{8}{5}$，-$\frac{24}{5}$），
过A₂作A₂P⊥A₂H，
∴∠A₁A₂P=∠ABK，
∵A₁A₂=$\sqrt{5}$，
∴A₂P=2，A₁P=1，
∴A₂（$\frac{2}{5}$，-$\frac{19}{5}$）
∵F（-$\frac{2}{3}$，$\frac{10}{3}$）
∴A₂F的解析式为y=-$\frac{107}{16}$x-$\frac{9}{8}$①，
∵B（2，0），D（0，-1），
∴直线BD解析式为y=$\frac{1}{2}$x-1②，
    联立①②得，x=-$\frac{2}{115}$，
∴N点的横坐标为：-$\frac{2}{115}$．
（3）∵C（0，3），B（2，0），D（0，-1）
∴CD=4，BC=$\sqrt{13}$，OB=2，
BC边上的高为DH，
根据等面积法得，$\frac{1}{2}$BC×DH=$\frac{1}{2}$CD×OB，
∴DH=$\frac{CD×OB}{BC}=\frac{4×2}{\sqrt{13}}$=$\frac{8\sqrt{13}}{13}$，
∵A（-4，0），C（0，3），
∴OA=4，OC=3，
∴tan∠ACD=$\frac{OA}{OC}=\frac{4}{3}$，
①当PC=PQ时，简图如图1，

过点P作PG⊥CD，过点D作DH⊥PQ，
∵tan∠ACD=$\frac{4}{3}$
∴设CG=3a，则QG=3a，PG=4a，PQ=PC=5a，
∴DQ=CD-CQ=4-6a
∵△PGQ∽△DHQ，
∴$\frac{PG}{DH}=\frac{PQ}{DQ}$，
∴$\frac{4a}{\frac{8\sqrt{13}}{13}}=\frac{5a}{4-6a}$，
∴a=$\frac{2}{3}-\frac{5\sqrt{13}}{39}$，
∴PC=5a=$\frac{10}{3}-\frac{25\sqrt{13}}{39}$；
②当PC=CQ时，简图如图2，

过点P作PG⊥CD，
∵tan∠ACD=$\frac{4}{3}$
∴设CG=3a，则PG=4a，
∴CQ=PC=5a，
∴QG=CQ-CG=2a，
∴PQ=2$\sqrt{5}$a，
∴DQ=CD-CQ=4-5a
∵△PGQ∽△DHQ，
同①的方法得出，PC=4-$\frac{4\sqrt{65}}{13}$，

③当QC=PQ时，简图如图1

过点Q作QG⊥PC，过点C作CN⊥PQ，
设CG=3a，则QG=4a，PQ=CQ=5a，
∴PG=3a，
∴PC=6a
∴DQ=CD-CQ=4-5a，
利用等面积法得，CN×PQ=PC×QG，
∴CN=$\frac{24}{5}$a，
∵△CQN∽△DQH
同①的方法得出PC=$\frac{24}{5}-\frac{10\sqrt{13}}{13}$
④当PC=CQ时，简图如图4，

过点P作PG⊥CD，过H作HD⊥PQ，
设CG=3a，则PG=4a，CQ=PC=5a，
∴QD=4+5a，PQ=4$\sqrt{5}$，
∵△QPG∽△QDH，
同①方法得出．CP=$\frac{8\sqrt{65}}{13}-4$
综上所述，PC的值为：$\frac{10}{3}-\frac{25\sqrt{13}}{39}$；4-$\frac{4\sqrt{65}}{13}$，$\frac{24}{5}-\frac{10\sqrt{13}}{13}$，=$\frac{8\sqrt{65}}{13}-4$．

点评 此题是二次函数综合题，主要考查了待定系数法，面积公式及计算方法，等腰三角形的性质，相似三角形的判定和性质，分情况讨论计算是解本题的关键，构造出相似三角形是解本题的难点．计算量较大．