
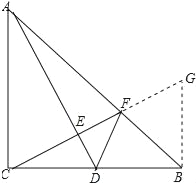
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,∠ABC=45°,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.

【答案】见解析
【解析】
作BG⊥CB,交CF的延长线于点G,由ASA证明△ACD≌△CBG,得出CD=BG,∠CDA=∠CGB,证出BG=BD,∠FBD=∠GBF=![]() ∠CBG,再由SAS证明△BFG≌△BFD,得出∠FGB=∠FDB,即可得出结论.
∠CBG,再由SAS证明△BFG≌△BFD,得出∠FGB=∠FDB,即可得出结论.
证明:作BG⊥CB,交CF的延长线于点G,如图所示:
∵∠CBG=90°,CF⊥AD,
∴∠CAD+∠ADC=∠BCG+∠ADC=90°,
∴∠CAD=∠BCG,
在△ACD和△CBG中,
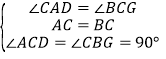 ,
,
∴△ACD≌△CBG(ASA),
∴CD=BG,∠CDA=∠CGB,
∵CD=BD,
∴BG=BD,
∵∠ABC=45°,
∴∠FBD=∠GBF=![]() ∠CBG,
∠CBG,
在△BFG和△BFD中,
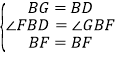 ,
,
∴△BFG≌△BFD(SAS),
∴∠FGB=∠FDB,
∴∠ADC=∠BDF.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
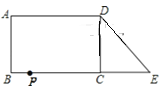
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
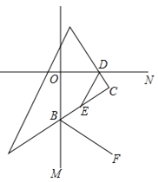
【题目】如图,直线OM⊥ON,垂足为O,三角板的直角顶点C落在∠MON的内部,三角板的另两条直角边分别与ON、OM交于点D和点B.
(1)填空:∠OBC+∠ODC= ;
(2)如图,若DE平分∠ODC,BF平分∠CBM,求证:DE⊥BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】振兴中学某班的学生对本校学生会倡导的“抗震救灾,众志成城”自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3∶4∶5∶8∶6,又知此次调查中捐款25元和30元的学生一共42人.

(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,则在①a<0,②b>0,③c<0,④b2﹣4ac>0中错误的个数为( )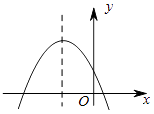
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学在点P处测得教学楼A位于北偏东60°方向,办公楼B位于南偏东45°方向.小明沿正东方向前进60米到达C处,此时测得教学楼A恰好位于正北方向.办公楼B正好位于正南方向.求教学楼A与办公楼B之间的距离 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:a*b=10a×10b,例如图3*4=103×104=107.
(1)试求12*3和2*5的值;
(2)想一想(a*b)*c与a*(b*c)相等吗?如果相等,请验证你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角梯形OABC中,CB∥OA,∠COA=90°,CB=3,OA=6,BA=3![]() .分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.
.分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.
(1)求点B的坐标;
(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F,过点E作EG⊥x轴于G,且EG:OG=2.求直线DE的解析式;
(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com