
分析 根据二次函数图象与一次函数图象的交点问题,通过解-2x+6=-2x2+4x+6可得到交点的横坐标,则可得到它们交点坐标为(0,6),(3,0);再根据抛物线与x轴的交点问题,通过解方程-2x2+4x+6得二次函数y2=-2x2+4x+6的图象与x轴的交点坐标为(-1,0),(3,0),然后大致画出两函数图象,再观察函数图象,找出一次函数图象在抛物线上方所对应的自变量的范围即可.
解答 解:解方程-2x+6=-2x2+4x+6得x1=0,x2=3,
所以一次函数y1=-2x+6的图象与二次函数y2=-2x2+4x+6的图象相交,交点坐标为(0,6),(3,0);
解方程-2x2+4x+6得x1=-1,x2=3,
所以二次函数y2=-2x2+4x+6的图象与x轴相交,交点坐标为(-1,0),(3,0),
如图,
当x<0或x>3时,y1>y2.
点评 本题考查了抛物线与x轴的交点:对于二次函数y=ax2+bx+c(a,b,c是常数,a≠0),△=b2-4ac决定抛物线与x轴的交点个数.解决此类问题的关键是把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为求方程ax2+bx+c=0的解的问题.也考查了二次函数图象与一次函数图象的交点问题.


科目:初中数学 来源: 题型:解答题
 请阅读下面材料:
请阅读下面材料:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
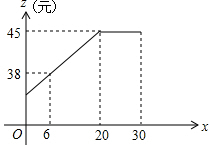 大学生李某毕业响应国家“自主创业”的号召,在我市沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日购进一种今年新上市的文具袋9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后得知日销售量y(个)与销售时间x(天)之间有如下关系:y=-2x+80(1≤x≤30,x取正整数);又知销售价格z(元/个)与销售时间x(天,x取正整数)之间的函数关系满足如图所示的函数图象.
大学生李某毕业响应国家“自主创业”的号召,在我市沙坪坝学校密集的沙南街路段投资开办了一个学生文具店.该店在开学前8月31日购进一种今年新上市的文具袋9月份(9月1日至9月30日)进行30天的试销售,购进价格为20元/个.销售结束后得知日销售量y(个)与销售时间x(天)之间有如下关系:y=-2x+80(1≤x≤30,x取正整数);又知销售价格z(元/个)与销售时间x(天,x取正整数)之间的函数关系满足如图所示的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com