
【题目】一位同学拿了两块45°的三角尺△MNK、△ACB做了一个探究活动:将△MNK的直角顶点M放在△ABC的斜边AB的中点处,设AC=BC=a.
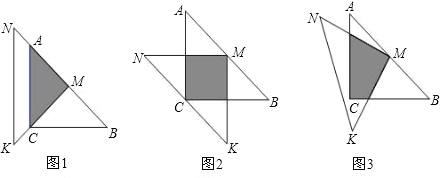
(1)如图1,两个三角尺的重叠部分为△ACM,则重叠部分的面积为 ,周长为 .
(2)将图1中的△MNK绕顶点M逆时针旋转45°,得到图2,此时重叠部分的面积为 ,周长为 .
2(3)如果将△MNK绕M旋转到不同于图1,图2的位置,如图3所示,猜想此时重叠部分的面积为多少?并试着加以验证.
【答案】(1)重叠部分的面积是△ACB的面积的一半为a2,周长为(1+)a.(2)边长为a,面积为a2,周长为2a.(3)![]() .
.
【解析】解:(1)∵AM=MC=![]() AC=
AC=![]() a,则
a,则
∴重叠部分的面积是△ACB的面积的一半为a2,周长为(1+)a.
(2)∵重叠部分是正方形
∴边长为a,面积为a2,周长为2a.
(3)猜想:重叠部分的面积为![]() .
.
理由如下:
过点M分别作AC、BC的垂线MH、MG,垂足为H、G
设MN与AC的交点为E,MK与BC的交点为F
∵M是△ABC斜边AB的中点,AC=BC=a
∴MH=MG=![]()
又∵∠HME+∠HMF=∠GMF+∠HMF,
∴∠HME=∠GMF,
∴Rt△MHE≌Rt△MGF
∴阴影部分的面积等于正方形CGMH的面积
∵正方形CGMH的面积是MGMH=![]() ×
×![]() =
=![]()
∴阴影部分的面积是![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,A、B分别是x轴上位于原点左右两侧的两点,点P(2,p)在第一象限内,直线PA交y轴与点C(0,2),直线PB交y轴与点D,且S△AOP=4,
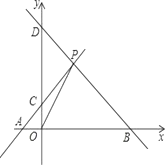
(1)求S△COP;
(2)求点A的坐标及p的值;
(3)若3S△AOP=S△BOP,求直线BD的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,直线AB分别与x轴、y轴交于点B和A,与反比例函数的图像交于C、D,CE⊥x轴于点E,若![]() ,OB=4,OE=2,点D的坐标为(6,m).
,OB=4,OE=2,点D的坐标为(6,m).
(1)求直线AB和反比例函数的解析式;
(2)求△OCD的面积。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于点C,点D,C关于抛物线的对称轴对称,直线AD与y轴相交于点E.
(1)求直线AD的解析式;
(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG⊥AD于点G,作FH平行于x轴交直线AD于点H,求△FGH周长的最大值;
(3)如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线AM对称,连接M Q′,P Q′.当△PM Q′与□APQM重合部分的面积是□APQM面积的![]() 时,求□APQM面积.
时,求□APQM面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点P到直线l的距离为3,以点P为圆心,r为半径画圆,如果圆上有且只有两点到直线L的距离均为2,则半径r的取值范围是( )
A.r>1
B.r>2
C.2<r<2
D.1<r<5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACD中,∠ADC=90°,AD=2,CD=1,点B在AD的延长线上,BD=l,连接BC.
(1)求BC的长;
(2)动点P从点A出发,向终点B运动,速度为1个单位/秒,运动时间为t秒.
①当t为何值时,△PDC≌△BDC;
②当t为何值时,△PBC是以PB为腰的等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小颖做掷骰子的游戏,规则如下:
① 游戏前,每人选一个数字;
② 每次同时掷两枚均匀骰子;
③ 如果同时掷得的两枚骰子点数之和,与谁所选数字相同,那么谁就获胜.
(1)在下表中列出同时掷两枚均匀骰子所有可能出现的结果:
第2枚骰子掷得 第1枚 的点数 骰子掷得的点数 | 1 | 2 | 3 | 4 | 5 | 6 |
1 | ||||||
2 | ||||||
3 | ||||||
4 | ||||||
5 | ||||||
6 |
(2)小明选的数字是5,小颖选的数字是6.如果你也加入游戏,你会选什么数字,使自
己获胜的概率比他们大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种衬衫能畅销市场,就用12000元购进了一批这种衬衫,上市后果然供不应求,商家又用了26400元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但每件进价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫都按每件150元的价格销售,则两批衬衫全部售完后的利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com