
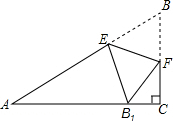
 如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形.
如图,在△ABC中,∠C=90°,点E,F分别在边AB,BC上,沿直线EF将△EBF翻折,使顶点B的对应点B1落在AC边上,且EB1⊥AC.求证:四边形BFB1E是菱形. 分析 首先证出EB1∥BC,由折叠的性质得:BE1=BE,∠EB1F=∠B,由角的互余关系证出∠A=∠FB1C,得出AB∥B1F,证出四边形四边形BFB1E是平行四边形,即可得出四边形BFB1E是菱形.
解答 证明:∵∠C=90°,
∴AC⊥BC,
∵EB1⊥AC,
∴EB1∥BC,
由折叠的性质得:BE1=BE,∠EB1F=∠B,
∵∠A+∠B=90°,∠EB1F+∠FB1C=90°,
∴∠A=∠FB1C,
∴AB∥B1F,
∴四边形四边形BFB1E是平行四边形,
又∵BE1=BE,
∴四边形BFB1E是菱形.
点评 本题考查了翻折变换的性质、菱形的判定、平行四边形的判定、平行线的判定;熟练掌握翻折变换的性质,证明AB∥B1F是解决问题的关键.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:选择题
 已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )
已知二次函数y=ax2+bx+c+2的图象如图所示,有下列4个结论:①abc<0;②b2=4ac;③a+c=b-2;④m(am+b)+b>a(m≠-1),其中结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
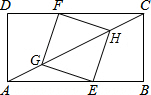 如果,矩形ABCD中,点E在AB上,点F在CD上,点G,H在对角线AC上,且CH=AG,CF=AE.
如果,矩形ABCD中,点E在AB上,点F在CD上,点G,H在对角线AC上,且CH=AG,CF=AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示).回答下列问题:
某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边周长为30米的篱笆围成.已知墙长为18米(如图所示).回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
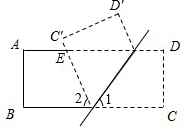 如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E.
如图,长方形纸片CD沿MN折叠(M,N在AD、BC上),AD∥BC,C′,D′为C、D的对称点,C′N交AD于E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com