
【题目】小虫从![]() 点出发在一条直线上来回爬行,假定向右爬行的路程记作正数,向左爬行的路程记作负数,爬行的各段路程(单位:
点出发在一条直线上来回爬行,假定向右爬行的路程记作正数,向左爬行的路程记作负数,爬行的各段路程(单位:![]() )依次为:
)依次为:![]() .
.
(1)小虫在爬行过程中离![]() 点最远的距离是多少?
点最远的距离是多少?
(2)小虫爬到最后距![]() 点多远?
点多远?
(3)如果小虫爬行![]() 就奖励它一粒芝麻,那么小虫一共可得到多少粒芝麻?
就奖励它一粒芝麻,那么小虫一共可得到多少粒芝麻?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)50
;(3)50
【解析】
(1)分别依次进行计算,根据绝对值的大小比较即可;(2)把所有的路程相加,然后根据有理数的加法运算法则进行计算即可;(3)根据绝对值的性质把所有路程相加;根据爬行就奖励即可得到答案;
解:
(1)(+5)+(-3)=2,
2+(+9)=11,
11+(-7)=4,
4+(-6)=-2,
-2+(+12)=10,
10+(-8)=2,
∴距离点A最远有11cm;
(2)5+(-3)+9+(-7)+(-6)+12+(-8)=2;
∴小虫爬到最后时离A点2cm;
(3) |+5|+|-3|+|+9|+|-7|+|-6|+|+12|+|-8|,
=5+3+9+7+6+12+8,
=50cm.
50×1=50(粒).
答:小虫共可以得到50粒芝麻.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中项点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式。请你观察下列儿种简单多面体模型,解答下列问题:

(1)根据上面多面体模型,完成表格中的空格:
多面体 | 项点数(V) | 面数(F) | 棱数(F) |
四面体 | |||
长方体 | |||
正八面体 | |||
正十二面体 |
你发现项点数(V)、面数(F)、棱数(F)之间存在的关系式是__________________________.
(2)一个多面体的面数比顶点数小8,且有30条棱,则这多面体的顶点数是 20;
(3)某个玻璃饰品的外形是简单多面体,它的外表是由三角形和八边形两种多边形拼接而成,且有48个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.
(1)求从袋中随机摸出一球,标号是1的概率;
(2)从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励节约用水,某地推行阶梯式水价计费制,标准如下:每月用水不超过17立方米的按每立方米![]() 元计费,超过17立方米而未超过30立方米的部分按每立方米
元计费,超过17立方米而未超过30立方米的部分按每立方米![]() 元计费,超过30立方米的部分按每立方米
元计费,超过30立方米的部分按每立方米![]() 元计费,某户居民上月用水35立方米,应缴水费_________元.
元计费,某户居民上月用水35立方米,应缴水费_________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
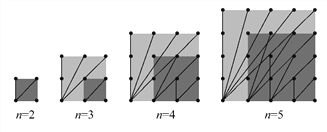
【题目】探索n×n的正方形钉子板上(n是钉子板每边上的钉子数,每边上相邻钉子间的距离为1),连接任意两个钉子所得到的不同长度值的线段种数:
当n=2时,钉子板上所连不同线段的长度值只有1与![]() ,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
,所以不同长度值的线段只有2种,若用S表示不同长度值的线段种数,则S=2;
当n=3时,钉子板上所连不同线段的长度值只有1, ![]() ,2,
,2, ![]() ,2
,2![]() 五种,比n=2时增加了3种,即S=2+3=5.
五种,比n=2时增加了3种,即S=2+3=5.
(1)观察图形,填写下表:
钉子数(n×n) | S值 |
2×2 | 2 |
3×3 | 2+3 |
4×4 | 2+3+(____) |
5×5 | (________) |
(2)写出(n-1)×(n-1)和n×n的两个钉子板上,不同长度值的线段种数之间的关系;(用式子或语言表述均可).
(3)对n×n的钉子板,写出用n表示S的代数式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学组织全校1000名学生进行了校园安全知识竞赛.为了解本次知识竞赛的成绩分布情况,从中随机抽取了部分学生的成绩(得分取正整数,满分为100分),并绘制了如图的频数分布表和频数分布直方图(不完整).
分组 | 频数 | 频率 |
50.5~60.5 | 10 | a |
60.5~70.5 | b | |
70.5~80.5 | 0.2 | |
80.5~90.5 | 52 | 0.26 |
90.5~100.5 | 0.37 | |
合计 | c | 1 |

请根据以上提供的信息,解答下列问题:
(1)直接写出频数分布表中a,b,c的值,补全频数分布直方图.
(2)上述学生成绩的中位数落在哪一组范围内?
(3)学校将对成绩在90.5~100.5分之间的学生进行奖励,请估计全校1000名学生中约有多少名获奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BD平分∠ABC,AE⊥BD于点O,交BC于点E,AD∥BC,连接CD.
(1)求证:AO=EO;
(2)若AE是△ABC的中线,则四边形AECD是什么特殊四边形?证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
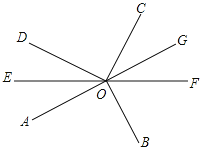
(1)∠AOD和∠BOC是否互补?说明理由;
(2)射线OF是∠BOC的平分线吗?说明理由;
(3)反向延长射线OA至点G,射线OG将∠COF分成了4:3的两个角,求∠AOD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com