
 置关系时的m的取值范围;
置关系时的m的取值范围;
| OE |
| O1M |
| OB |
| BM |
| m |
| 3 |
| 2 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |

| O1M |
| BO1 |
| 3 |
| 5 |
| BM |
| BO1 |
| 4 |
| 5 |
| 5 |
| 2 |
| 12 |
| 5 |
| EH |
| BE |
| ||
|
| 24 |
| 25 |
| 24 |
| 25 |
| 3 |
| 5 |
| 4 |
| 5 |


科目:初中数学 来源:不详 题型:解答题
 小时)的函数关系图象,假设两种灯的使用寿命都是2000小时,照明效果一样.(费用=灯的售价+电费)
小时)的函数关系图象,假设两种灯的使用寿命都是2000小时,照明效果一样.(费用=灯的售价+电费)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
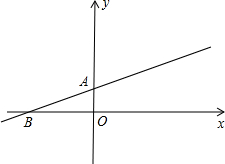 为圆心的圆与x轴相切于点C.
为圆心的圆与x轴相切于点C.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题


查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 3 |
| 4 |
 点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.
点,将△AOB绕点O顺时针旋转90°后得到△A′OB′.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com