
【题目】已知抛物线![]() 经过点A(3,0),B(﹣1,0).
经过点A(3,0),B(﹣1,0).
(1)求抛物线的解析式;
(2)求抛物线的顶点坐标.
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】点C是直线l1上一点,在同一平面内,把一个等腰直角三角板ABC任意摆放,其中直角顶点C与点C重合,过点A作直线l2⊥l1,垂足为点M,过点B作l3⊥l1,垂足为点N
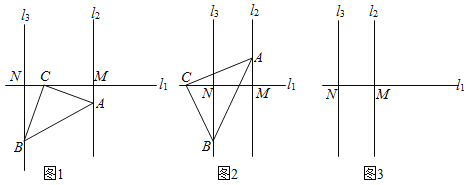
(1)当直线l2,l3位于点C的异侧时,如图1,线段BN,AM与MN之间的数量关系 (不必说明理由);
(2)当直线l2,l3位于点C的右侧时,如图2,判断线段BN,AM与MN之间的数量关系,并说明理由;
(3)当直线l2,l3位于点C的左侧时,如图3,请你补全图形,并直接写出线段BN,AM与MN之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数 y ax2 2a 1x a 1a 0,有下列结论:①其图象与 x 轴一定相交;②若 a 0 , 函数在 x 1 时,y 随 x 的增大而减小;③无论 a 取何值,抛物线的顶点始终在同一条直线上;④无论 a 取何值,函数图象都经过同一个点.其中所有正确的结论是:( )
A. ①②③ B. ①③④ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD是△ABC的角平分线,AD的中垂线交AB于点F,交BC的延长线于点E.以下四个结论:(1)∠EAD=∠EDA;(2)DF∥AC;(3)∠FDE=90°;(4)∠B=∠CAE.恒成立的结论有( )

A. (1)(2)B. (2)(3)(4)C. (1)(2)(4)D. (1)(2)(3)(4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰Rt△ABC和△CDE,AC=BC,CD=CE,连接BE、AD,P为BD中点,M为AB中点、N为DE中点,连接PM、PN、MN.
(1)试判断△PMN的形状,并证明你的结论;
(2)若CD=5,AC=12,求△PMN的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,点D,E是边BC上的两点,且AB=BE,AC=CD.
(1)若∠BAC =90°,求∠DAE的度数;
(2)若∠BAC=120°,直接写出∠DAE的度数
(3)设∠BAC=α,∠DAE=β,猜想α与β的之间数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,正方形A的一个顶点与正方形B的对称中心重合,重叠部分面积是正方形A面积的![]() ,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的( )
,如图②,移动正方形A的位置,使正方形B的一个顶点与正方形A的对称中心重合,则重叠部分面积是正方形B面积的( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
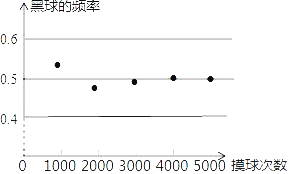
【题目】一个不透明的袋子里装有黑白两种颜色的球其40只,这些球除颜色外都相同.小明从袋子中随机摸一个球,记下颜色后放回,不断重复,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
(1)摸到黑球的频率会接近 (精确到0.1);
(2)估计袋中黑球的个数为 只:
(3)若小明又将一些相同的黑球放进了这个不透明的袋子里,然后再次进行摸球试验,当重复大量试验后,发现黑球的频率稳定在0.6左右,则小明后来放进了 个黑球.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车去郊外春游,他离家的距离y(千米)与所用时间x(小时)之间的关系如图,根据图象回答:
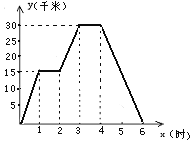
(1)小明到达离家最远的地方需几小时?此时离家多远?
(2)小明出发两个半小时时离家多远?
(3)小明出发多长时间离家12.5千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com