
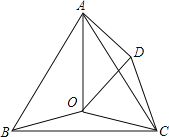
【题目】如图,O是等边三角形ABC内一点,∠AOB=110°,∠BOC=m°,D是△ABC外一点,且△ADC≌△BOC,连接OD.当m为_____时,△AOD是等腰三角形.
【答案】110或125或140.
【解析】
根据全等三角形的性质得到∠OCB=∠DCA,CO=CD,证明∠DCA+∠ACO=60°,根据等边三角形的判定定理证明△COD是等边三角形,然后分AD=AO、DA=DO、OD=AO三种情况,根据等腰三角形的性质,三角形内角和定理计算.
∵△ADC≌△BOC,
∴∠ADC=∠BOC=m°,∠OCB=∠DCA,CO=CD,
∵△ABC是等边三角形,
∴∠ACB=60°,即∠OCB+∠ACO=60°,
∴∠DCA+∠ACO=60°,又CO=CD,
∴△COD是等边三角形,
∴∠COD=∠CDO=60°;
∴∠AOD=360°-∠AOB-∠BOC-∠COD=360°-110°-m°-60°=190°-m°,
∠ADO=∠ADC-∠CDO=m°-60°,
∴∠OAD=180°-∠AOD-∠ADO=180°-(m°-60°)-(190°-m°)=50°,
若AD=AO,则∠ADO=∠AOD,即m°-60°=190°-m°,
解得:m°=125°;
若OA=OD,则∠ADO=∠OAD,则m°-60°=50°,
解得:m°=110°;
若DA=DO,则∠OAD=∠AOD,即50°=190°-m°,
解得:m°=140°;
综上所述,当m为125或110或140时,△AOD是等腰三角形,
故答案为110或125或140.


科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为
(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为![]() ,直线l的解析式为y=x.
,直线l的解析式为y=x.
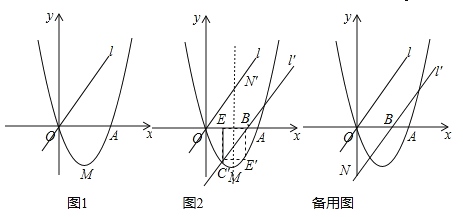
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
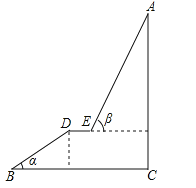
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
科目:初中数学 来源: 题型:
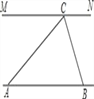
【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行
河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,
沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为矩形,H、F分别为AD、BC边的中点,四边形EFGH为矩形,E、G分别在AB、CD边上,则图中四个直角三角形面积之和与矩形EFGH的面积之比为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
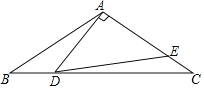
A. 17.5° B. 12.5° C. 12° D. 10°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出的以下四个结论:①AE=CF; ②△EPF一定是等腰直角三角形; ③S四边形AEPF=![]() S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)
S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数y=3x与反比例函数y=![]() 的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
的图象交于A,B两点,点A的横坐标为2,AC⊥x轴,垂足为C,连接BC.
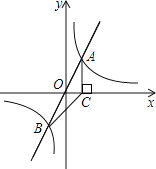
(1)求反比例函数的表达式;
(2)求△ABC的面积;
(3)若点P是反比例函数y=![]() 图象上的一点,△OPC与△ABC面积相等,请直接写出点P的坐标.
图象上的一点,△OPC与△ABC面积相等,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 △ABC和 △ADE中,∠BAD=∠CAE, ∠ABC=∠ADE.
(1)写出图中两对相似三角形(不得添加字母和线);
(2)请证明你写出的两对相似三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com