
分析 结合分式混合运算的运算法则进行求解即可.
解答 解:(1)$\frac{-3ab}{{4{x^2}y}}÷\frac{21b}{10xy}$
=$\frac{-3ab}{4{x}^{2}y}$×$\frac{10xy}{21b}$
=-$\frac{5a}{14x}$.
(2)$\frac{1}{{{{(x-y)}^2}}}+\frac{2}{{{x^2}-3xy+2{y^2}}}$
=$\frac{1}{(x-y)^{2}}$+$\frac{2}{(x-y)(x-2y)}$
=$\frac{x-2y}{(x-y)^{2}(x-2y)}$+$\frac{2(x-y)}{(x-y)^{2}(x-2y)}$
=$\frac{3x-4y}{(x-y)^{2}(x-2y)}$.
点评 本题考查了分式的混合运算,解答本题的关键在于熟练掌握分式混合运算的运算法则.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
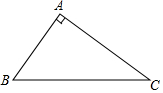 如图,已知△ABC中,已知△ABC中,∠BAC=90°,∠ABC=54°,AC=10.
如图,已知△ABC中,已知△ABC中,∠BAC=90°,∠ABC=54°,AC=10.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
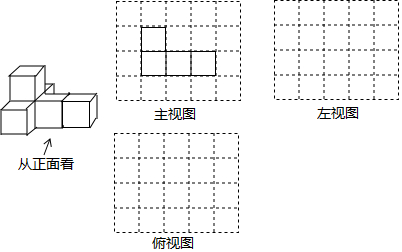
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF.
如图1,在正方形ABCD中,E、F分别为DC、BC边上的点,且满足∠EAF=45°,连结EF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
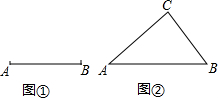 定义:如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“奇异三角形”,这条中线为“奇异中线”.
定义:如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“奇异三角形”,这条中线为“奇异中线”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com