
 如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.
如图,在Rt△ABC中,∠C=90°,AC=8m,BC=6m,点P由C点出发以2m/s的速度向终点A匀速移动,同时点Q由点B出发以1m/s的速度向终点C匀速移动,当一个点到达终点时另一个点也随之停止移动.分析 (1)分别表示出线段PC和线段CQ的长后利用S△PCQ=$\frac{1}{3}$S△ABC列出方程求解;
(2)设运动时间为ts,△PCQ与△ACB相似,当△PCQ与△ACB相似时,可知∠CPQ=∠A或∠CPQ=∠B,则有$\frac{CP}{CA}$=$\frac{CQ}{CB}$或$\frac{CP}{CB}$=$\frac{CQ}{CA}$,分别代入可得到关于t的方程,可求得t的值;
解答 解:(1)设经过x秒△PCQ的面积为△ACB的面积的$\frac{1}{3}$,
由题意得:PC=2xm,CQ=(6-x)m,
则$\frac{1}{2}$×2x(6-x)=$\frac{1}{3}$×$\frac{1}{2}$×8×6,
解得:x=2或x=4.
则经过2秒或4秒,△PCQ的面积为△ACB的面积的$\frac{1}{3}$;
(2)设运动时间为ts,△PCQ与△ACB相似.
当△PCQ与△ACB相似时,则有$\frac{CP}{CA}$=$\frac{CQ}{CB}$或$\frac{CP}{CB}$=$\frac{CQ}{CA}$,
所以$\frac{2t}{8}$=$\frac{6-t}{6}$,或$\frac{2t}{6}$=$\frac{6-t}{8}$,
解得t=$\frac{12}{5}$,或t=$\frac{18}{11}$.
因此,经过$\frac{12}{5}$秒或$\frac{18}{11}$秒,△OCQ与△ACB相似;
点评 本题考查了一元二次方程的应用,用到的知识点是相似三角形的判定与性质,三角形的面积,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,△ABC经过平移得到△A1B1C1,B1C=6cm,BC=3.5cm,则BC1=1cm;若∠B1=90°,∠A=60°,则∠A1C1B1=30°.
如图,△ABC经过平移得到△A1B1C1,B1C=6cm,BC=3.5cm,则BC1=1cm;若∠B1=90°,∠A=60°,则∠A1C1B1=30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,C,E,F为⊙O上的点,CA是∠BAF的平分线,过点C作CD⊥AF交AF的延长线于D点,CE⊥AB,垂足为点G.
如图,AB是⊙O的直径,C,E,F为⊙O上的点,CA是∠BAF的平分线,过点C作CD⊥AF交AF的延长线于D点,CE⊥AB,垂足为点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
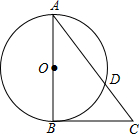 如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$.
如图,△ABC是Rt△,∠ABC=90°,以AB为直径的⊙O交AC于D,⊙O的半径为5,$tanA=\frac{3}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的网格中,每个小正方形的边长都为1.
在如图所示的网格中,每个小正方形的边长都为1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k<0)的图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,则k的值是-3.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{4}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k<0)的图象于点B,BC⊥x轴,若S△ABC=$\frac{15}{2}$,则k的值是-3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com