
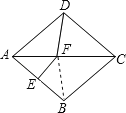
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于 .

【答案】60°
【解析】
试题分析:连接BF,根据菱形的对角线平分一组对角求出∠BAC,∠BCF=∠DCF,四条边都相等可得BC=DC,再根据菱形的邻角互补求出∠ABC,然后根据线段垂直平分线上的点到线段两端点的距离相等可得AF=BF,根据等边对等角求出∠ABF=∠BAC,从而求出∠CBF,再利用“边角边”证明△BCF和△DCF全等,根据全等三角形对应角相等可得∠CDF=∠CBF.
解:如图,连接BF,
在菱形ABCD中,∠BAC=![]() ∠BAD=
∠BAD=![]() ×80°=40°,∠BCF=∠DCF,BC=DC,
×80°=40°,∠BCF=∠DCF,BC=DC,
∠ABC=180°﹣∠BAD=180°﹣80°=100°,
∵EF是线段AB的垂直平分线,
∴AF=BF,∠ABF=∠BAC=40°,
∴∠CBF=∠ABC﹣∠ABF=100°﹣40°=60°,
∵在△BCF和△DCF中,
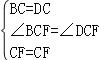 ,
,
∴△BCF≌△DCF(SAS),
∴∠CDF=∠CBF=60°,
故答案为:60°.


科目:初中数学 来源: 题型:
【题目】已知∠A=45°15′,∠B=45°12′18″,∠C=45.15°,则 ( )
A. ∠A>∠B>∠C B. ∠B>∠A>∠C
C. ∠A>∠C>∠B D. ∠C>∠A>∠B
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)|-1|+(—2)3+(7-π)0-(![]() )-1;
)-1;
(2) (-2a)3·(a2)2÷a3
(3) (3a+b-2)(3a-b+2)
(4)10002-1002×998
(5) (x+1)(x2+1)(x4+1)(x-1)
(6) (3a+2)2(3a-2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】算式(﹣7)+(+1)﹣(﹣3)﹣(+5)写成省略括号的和的形式,正确的是( )
A. 7+1+3﹣5 B. ﹣7+1+3﹣5 C. ﹣7+1﹣3﹣5 D. ﹣7+1+3+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要使函数y=(m﹣2)xn﹣1+n是一次函数,应满足( )
A. m≠2,n≠2 B. m=2,n=2 C. m≠2,n=2 D. m=2,n=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在射线OA上,CE平分∠ACD. OF平分∠COB并与射线CD交于点F。
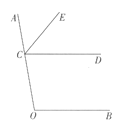
(1)依题意补全图形;
(2)若∠COB+∠OCD=180°,求证:∠ACE=∠COF。
请将下面的证明过程补充完整。
证明:∵CE平分∠ACD,OF平分∠COB,
∴∠ACE=______________,∠COF=![]() ∠COB。
∠COB。
(理由: _____________________________________)
∵点C在射线OA上,
∴∠ACD+∠OCD=180°。
∵∠COB+∠OCD=180°,
∴∠ACD=∠____________。
(理由: ___________________________________)
∴∠ACE=∠COF。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com