
 距沿海某城市A的正南方向200km的B处有一台风中心,根据海事预报,以台风中心为圆心,250km为半径的圆形区域内会受到台风影响,该台风中心现在正以25km/h的速度沿北偏东45°方向往C移动,问:
距沿海某城市A的正南方向200km的B处有一台风中心,根据海事预报,以台风中心为圆心,250km为半径的圆形区域内会受到台风影响,该台风中心现在正以25km/h的速度沿北偏东45°方向往C移动,问:分析 (1)过A作AD⊥BC于D,根据勾股定理求出AD,比较即可;
(2)求出BG的长,根据速度求出时间.
解答 解:(1)过A作AD⊥BC于D,
根据点与线段之间垂线段最短的定理,
AD即为A点到线段BC的最短距离,
在直角△ABD中,
∠B=45°,AB=200km,
则∠BAD=∠B,即AD=BD,
根据勾股定理AD2+BD2=AB2,
解得AD=100$\sqrt{2}$km,
AD<250km,
故A城市会收到台风影响;
(2)由题意得AG=250km,
由勾股定理得,DG=$\sqrt{A{G}^{2}-A{D}^{2}}$=50$\sqrt{17}$,
则BG=100$\sqrt{2}$+50$\sqrt{17}$,
故受影响时间为:(100$\sqrt{2}$+50$\sqrt{17}$)÷25=4$\sqrt{2}$+2$\sqrt{17}$h.
点评 本题考查的是解直角三角形的应用-方向角问题,正确理解方向角的概念、熟记锐角三角函数的定义是解题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:选择题
| A. | 3.4×103 | B. | 34×103 | C. | 0.34×103 | D. | 3.4×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
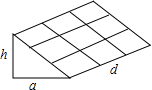 如图,要修建一个育苗棚,棚高h=3m,棚宽a=4m,棚长d=12m,现要在育苗棚的整个表面(除底面外所有的面)覆盖一层塑料薄膜,试求至少需要多少平方米塑料薄膜?(接缝处不计)
如图,要修建一个育苗棚,棚高h=3m,棚宽a=4m,棚长d=12m,现要在育苗棚的整个表面(除底面外所有的面)覆盖一层塑料薄膜,试求至少需要多少平方米塑料薄膜?(接缝处不计)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
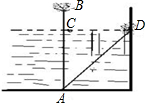 水池中离岸边D点1.5米的C处,直立长着一根芦苇,出水部分BC的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.
水池中离岸边D点1.5米的C处,直立长着一根芦苇,出水部分BC的长是0.5米,把芦苇拉到岸边,它的顶端B恰好落到D点,并求水池的深度AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,用直尺和圆规作∠PCD=∠AOB,作图痕迹中,弧$\widehat{MN}$是( )
如图,用直尺和圆规作∠PCD=∠AOB,作图痕迹中,弧$\widehat{MN}$是( )| A. | 以点C为圆心,OE为半径的弧 | B. | 以点C为圆心,EF为半径的弧 | ||
| C. | 以点G为圆心,OE为半径的弧 | D. | 以点G为圆心,EF为半径的弧 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
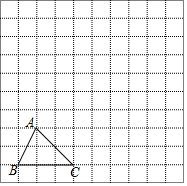 如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点时网格线的交点)
如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点时网格线的交点)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a-3>b-3 | B. | -3a<-3b | C. | a+3>b+3 | D. | $\frac{a}{3}$<$\frac{b}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com