【题目】如图二次函数 
的图象经过A（－1，0）和B（3，0）两点，且交 
轴于点C．
（1）试确定 
、 
的值；
（2）若点M为此抛物线的顶点，求△MBC的面积．
【答案】
（1）解：把（-1，0）、（3，0）代入y=x2+bx+c中，得
，
解得 
，
故b=-2，c=-3；
（2）解： 过M作MD垂直于y轴，垂足为D．求出抛物线的顶点 
；
△MBC的面积=梯形MDOB-△OBC-△CMD
= 
=3．
【解析】（1）将点A、B两点坐标代入函数解析式，建立关于b、c的方程组，解方程组即可求出b、c的值。
（2）过点过M作MD垂直于y轴，垂足为D．由△MBC的面积=梯形MDOB-△OBC-△CMD；或过点M作x轴的垂线交BC于点N，根据△MBC的面积=△CNM的面积+△MBN的面积。
【考点精析】关于本题考查的解二元一次方程组和三角形的面积，需要了解二元一次方程组：①代入消元法；②加减消元法；三角形的面积=1/2×底×高才能得出正确答案．
科目：初中数学 来源： 题型：
【题目】如图，EF∥AD，∠1=∠2．证明：∠DGA+∠BAC=180°．请完成说明过程．
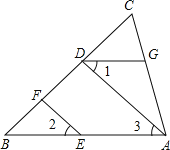
解：∵EF∥AD，（已知）
∴∠2=∠3．（ ）
又∵∠1=∠2（已知）
∴∠1=∠3，（等量代换）
∴AB∥ ，（ ）
∴∠DGA+∠BAC=180°．（ ）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】数学家华罗庚在一次出国访问途中，看到飞机上邻座的乘客阅读的杂志上有一道智力题：求59319的立方根．华罗庚脱口而出：39．众人感觉十分惊奇，请华罗庚给大家解读其中的奥秘．
你知道怎样迅速准确的计算出结果吗？请你按下面的问题试一试：
①
，又
，
，∴能确定59319的立方根是个两位数．
②∵59319的个位数是9，又
，∴能确定59319的立方根的个位数是9．
③如果划去59319后面的三位319得到数59，
而
，则
，可得
，
由此能确定59319的立方根的十位数是3
因此59319的立方根是39．
（1）现在换一个数195112，按这种方法求立方根，请完成下列填空．
①它的立方根是_______位数．
②它的立方根的个位数是_______．
③它的立方根的十位数是__________．
④195112的立方根是________．
（2）请直接填写结果：
①
________．
②
________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】李红在学校的研究性学习小组中负责了解初一年级200名女生掷实心球的测试成绩．她从中随机调查了若干名女生的测试成绩（单位：米），并将统计结果绘制成了如下的统计图表（内容不完整）．
测试成绩 |
|
|
|
|
| 合计 |
频数 | 3 | 27 | 9 | m | 1 | n |
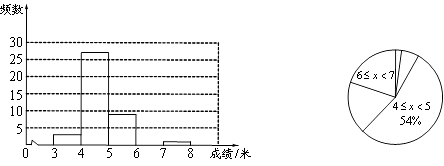
请你结合图表中所提供的信息，回答下列问题：
（1）表中m= ， n=；
（2）请补全频数分布直方图；
（3）在扇形统计图中， 
这一组所占圆心角的度数为度；
（4）如果掷实心球的成绩达到6米或6米以上为优秀，请你估计该校初一年级女生掷实心球的成绩达到优秀的总人数．
查看答案和解析>>
科目：初中数学 来源： 题型：
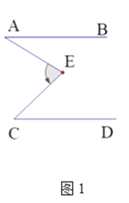
【题目】如图，AB∥CD．
（1）如图1，若∠A=35°，∠C=48°则∠E= °．
（2）如图2，若∠E＝120°，∠C＝110°，求∠A+∠F的度数；
（3）如图3，若∠E＝110°，
，若GD∥FC，请直接写出∠AGF与∠GDC的数量关系： ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，平行四边形ABCD中，AB⊥AC，AB=2，AC=4．对角线AC，BD相交于点O，将直线AC绕点O顺时针旋转α°，分别交直线BC、AD于点E、F．
（1）当α= °，四边形ABEF是平行四边形；
（2）在旋转的过程中，从A、B、C、D、E、F中任意4个点为顶点构造四边形．
①α= °，构造的四边形是菱形；
②若构造的四边形是矩形，求出该矩形的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
