解:(1)由B(3,m)可知OC=3,BC=m,
又∵△ABC为等腰直角三角形,
∴AC=BC=m,OA=m-3,
∴点A的坐标是(3-m,0),
∵∠ODA=∠OAD=45°,
∴OD=OA=m-3,
则点D的坐标是(0,m-3);
(2)又抛物线顶点为P(1,0),且过点B、D,
所以可设抛物线的解析式为:y=a(x-1)
2,
将D,B坐标代入:a(3-1)
2=m,a(0-1)
2=m-3,
得:a=1,m=4,
∴抛物线的解析式为y=x
2-2x+1,
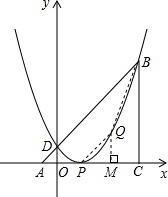
B坐标(3,4),A(-1,0);
(3)如图,过点Q作QM⊥AC于点M,设点Q的坐标是(x,x
2-2x+1),
则PM=(x-1),QM=x
2-2x+1,MC=(3-x),
∴S
四边形ABQP=S
△ABC-S
△PQM-S
梯形BCMQ,
=

×4×4-

•(x-1)•( x
2-2x+1)-

•(3-x)•( x
2-2x+1+4)
=-x
2+4x+1
=-(x-2)
2+5,
所以当x=2时,四边形ABQP的面积最大为5.
分析:(1)根据点C的坐标求出OC、BC的长度,再根据等腰直角三角形的两直角边相等可定的AC=BC,然后求出OA的长度,从而得到点A的坐标,再根据∠OAD=45°求出OD=OA,从而得到点D的坐标;
(2)利用顶点式设出二次函数解析式,然后把点B、D的坐标代入,根据待定系数法求解即可;
(3)根据抛物线解析式设出点Q的坐标,然后过点Q作QM⊥AC于点M,再根据S
四边形ABQP=S
△ABC-S
△PQM-S
梯形BCMQ,然后根据三角形的面积公式以及梯形的面积公式列式整理,再根据二次函数的最值问题求解即可.
点评:本题是对二次函数的综合考查,点的坐标,等腰直角三角形的性质,待定系数法求函数解析式,二次函数的最值问题,以及三角形的面积,梯形的面积公式,难点在于用字母表示数,以及利用“割补法”求不规则图形的面积,需熟练掌握.

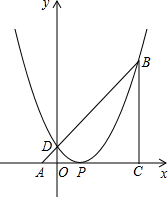 如图,△ABC中,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.
如图,△ABC中,∠ACB=90°,AC=BC,点A、C在x轴上,点B坐标为(3,m)(m>0),线段AB与y轴相交于点D,以P(1,0)为顶点的二次函数图象经过点B、D.
 ×4×4-
×4×4- •(x-1)•( x2-2x+1)-
•(x-1)•( x2-2x+1)- •(3-x)•( x2-2x+1+4)
•(3-x)•( x2-2x+1+4)

 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案 已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.
已知,如图,△ABC中,点D在BC上,且∠1=∠C,∠2=2∠3,∠BAC=70°.