Question

14．已知：如图，△ABC是边长为6cm的等边三角形，点P、Q分别是边AB、AC上的动点
（1）若点P在AB上以2cm/s的速度由点A向点B运动，同时点Q在AC上以1cm/s的速度由点C向点A运动，设点P运动时间为t秒
①试求当t为何值时，△APQ为等边三角形？
②若△APQ为直角三角形，试求t的值
（2）如图2，点D在△ABC外一点，且BD=CD，∠BDC=120°，若点P、Q在运动过程中始终保持∠PDQ=60°，试判断在这一过程中，△APQ的周长是否发生变化？若没有变化，请求出其周长；若发生变化，请说明理由．

Answer 1

分析 （1）根据运动得出AP=2t，CQ=t，AQ=6-t最后用等边三角形的性质即可列出方程求解即可；
（2）由∠BAC=60°，分两种情况AP=2AQ和AQ=2AP列出方程求解即可；
（3）先判断出点P，Q的运动情况，然后求出AP+AQ，再判断出PQ的变化情况，即可得出结论．

解答 解：（1）①∵△ABC是边长为6cm的等边三角形，
∴∠BAC=60°，
∵△APQ为等边三角形，
∴AP=AQ，
由运动知，AP=2t，CQ=t，
∴AQ=6-t，
∴2t=6-t，
∴t=2，
即：t=2时，△APQ为等边三角形；
②∵△APQ为直角三角形，∠BAC=60°，
由运动知，AP=2t，CQ=t，∴AQ=6-t，
Ⅰ、当∠APQ=90°时，∠AQP=30°，
∴AQ=2AP，
∴6-t=4t，
∴t=$\frac{6}{5}$，
Ⅱ、当∠AQP=90°时，∠APQ=30°，
∴AP=2AQ，
∴2t=2（6-t），
∴t=3，
即：△APQ为直角三角形时，t的值为$\frac{6}{5}$s或3s；
（3）△APQ的周长是发生变化，
理由：如图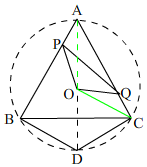，∵△ABC是等边三角形，
∴∠BAC=60°，
∵∠BDC=120°，
∴点D在△ABC的外接圆O上，
∵BD=CD，
∴点D必在AO的延长线上，
连接OC，
∴OA=OC，∠BAO=∠DAC=∠BCO=∠ACO=30°，
∴∠AOC=120°，
∵点P、Q在运动过程中始终保持∠PDQ=60°，
∴点P，Q是△AOC绕点O旋转和AB与AC的交点，
∵∠POQ=120°，
∴∠AOP=∠COQ，
在△AOP和△COQ中，$\left\{\begin{array}{l}{∠BAO=∠ACO=30°}\\{OA=OC}\\{∠AOP=∠COQ}\end{array}\right.$，
∴△AOP≌△COQ，
∴AP=CQ，PO=QO，
∴AP+AQ=CQ+AQ=AC=6，
∵$\frac{OA}{OC}=1$，$\frac{OP}{OQ}=1$，
∴$\frac{OA}{OC}=\frac{OP}{OQ}$，
∴$\frac{OA}{OP}=\frac{OC}{OQ}$，∵∠AOC=∠POQ，
∴△AOC∽△POQ，
∴$\frac{AC}{PQ}=\frac{OA}{OP}$，
∴PQ=$\frac{OP}{OA}•AC$=$\frac{6OP}{OA}$，
∵点O是边长为6的等边三角形ABC的外心，
∴OA=2$\sqrt{3}$，
∴PQ=$\sqrt{3}$OP，
∴△APQ的周长=AP+AQ+PQ=6+$\sqrt{3}$OP，
而P，Q在运动的过程中，OP由接近于2$\sqrt{3}$逐点减小到最小$\sqrt{3}$，再逐点最大到接近于2$\sqrt{3}$，
∴△APQ的周长的范围为9到12，（包括9但不包括12）．
即：△APQ的周长是发生变化，有最小值9．

点评 此题是三角形综合题，主要考查了等边三角形的性质，全等三角形的判定和性质，相似三角形的判定和性质，含30°的直角三角形的性质，三角形的外心，解本题的关键是判断出点D是△ABC的外接圆上，且在AO的延长线上，是一道中等难度的中考常考题，