
【题目】如图,设P是等边△ABC内的一点,PA=3,PB=5,PC=4,则∠APC=_______°.

【答案】150
【解析】
将△ABP绕点A逆时针旋转60°得△CEA,根据旋转的性质得EC=BP=5,AE=AP=3,∠PAE=60°,则△APE为等边三角形,得到PE=PA=3,∠APE=60°,在△EPC中,PE=3,PC=4,EC=5,根据勾股定理的逆定理可得到△EPC为直角三角形,且∠CPE=90°,即可得到∠APC的度数.
∵△ABC为等边三角形,
∴BA=BC,
可将△ABP绕点A逆时针旋转60°,得△CEA,
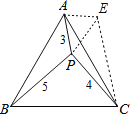
连EP,如图,
∴EC=BP=5,AE=AP=3,∠PAE=60°,
∴△APE为等边三角形,
∴PE=PA=3,∠APE=60°,
在△EPC中,PE=3,PC=4,EC=5,
∴![]()
∴△EPC为直角三角形,且∠CPE=90°,
∴![]()
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】图甲和图乙分别是A,B两家酒店去年下半年的月营业额(单位:百万元)统计图.
A酒店去年下半年的月营业额扇形统计图 B酒店去年下半年的月营业额
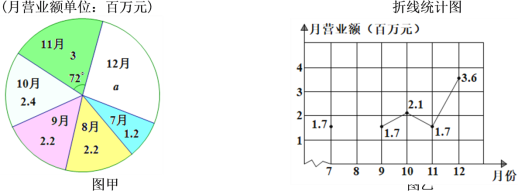
(1)求A酒店12月份的营业额a的值.
(2)已知B酒店去年下半年的月平均营业额为2.3百万元,求8月份的月营业额,并补全折线统计图.
(3)完成下面的表格(单位:百万元)
平均数 | 中位数 | 众数 | 方差 | |
A酒店 | 2.3 | 2.2 | 0.73 | |
B酒店 | 2.3 | 0.55 |
(4)综合以上分析,你认为哪一些数据更能较为准确的反映酒店的经营业绩?你认为哪家酒店的经营状况较好?请简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB//CD,(1)如图,若 E 为 DC 延长线上一点,AF、CG 分别为∠BAC、∠ACE 的平分线, 求证:AF//CG.

(2)若 E 为线段 DC 上一点(E 不与 C 重合),AF、CG 分别为∠BAC、∠ACE
的平分线,画出图形,试判断 AF,CG 的位置关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:①(![]() 0
0![]() )-1
)-1![]() 2017
2017![]() )2018 ; ②
)2018 ; ②![]() a3b2c4)3
a3b2c4)3![]() 2)2;
2)2;
③(x+3)(x![]() )(x2
)(x2![]() ) ; ④ 19982+7992+22(用公式计算).
) ; ④ 19982+7992+22(用公式计算).
(2)(2a+b)(2ab)(a2b)2+(6a44a2)÷(2a2),其中a=![]() ,b=1.
,b=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
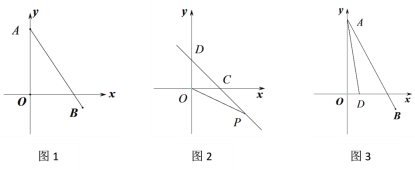
【题目】如图,射线AB∥CD,P为一动点,∠BAP与∠DCP的平分线AE与CE交于点E.
(1)当P在线段AC上运动时(如图1),即∠APC=180,则∠AEC=______;
(2)当P运动到图2的位置时,猜想∠AEC与∠APC 的关系,并说明理由;
(3)当P运动到图3的位置时,(2)中的结论还成立吗?(不要求说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在4×4的方格纸中,△ABC的三个顶点都在格点上.
(1)在图1中,画出一个与△ABC成中心对称的格点三角形;
(2)在图2中,画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形;
(3)在图3中,画出△ABC绕着点C按顺时针方向旋转90°后的三角形;
(4)在图4中,画出所有格点△BCD,使△BCD为等腰直角三角形,且S△BCD=4.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中,能判定四边形ABCD为平行四边形的个数是( )
①AB∥CD,AD=BC ; ②AB=CD,AD=BC;③∠A=∠B,∠C=∠D; ④AB=AD,CB=CD.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=![]() +
+![]() -1.
-1.
(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com