
| A. | -1<S<0 | B. | -2<S<0 | C. | -2<S<-1 | D. | -1<S<1 |
分析 首先根据二次函数y=ax2+bx+c的顶点在第三象限,且其图象过点(1,0)、(0,-1),判断出抛物线开口向上,所以a>0;再根据对称轴在y轴的左边,判断出b>0;然后图象过点(1,0)、(0,-1),判断出b=1-a,c=-1,再根据b>0,判断出a的取值范围,即可判断出s=a-b+c的值的变化范围.
解答 解:∵二次函数y=ax2+bx+c的顶点在第三象限,且其图象过点(1,0)、(0,-1),
∴抛物线开口向上,
∴a>0;
∵x=-$\frac{b}{2a}$<0,
∴b>0;
∵图象过点(1,0)、(0,-1),
∴$\left\{\begin{array}{l}{a+b+c=0}\\{c=-1}\end{array}\right.$
∴b=1-a,c=-1,
∵b>0,
∴1-a>0,
∴a<1,
又∵a>0,
∴0<a<1,
∴0<2a<2,
∴-2<2a-2<0,
∵s=a-b+c=a-(1-a)-1=2a-2,
∴-2<S<0.
故选:B.
点评 此题主要考查了二次函数的图象与系数的关系,要熟练掌握,解答此题的关键是要明确:①二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;②一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点. 抛物线与y轴交于(0,c).


科目:初中数学 来源: 题型:解答题
 在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.
在一次测量活动中,同学们想测量一条河的宽度,如图,他们选取了河岸上距离河岸边D处3m的B点作为观测点,此时身高AB=1.5m的小敏站在B处,恰好能看见河正对岸边上的电线杆GM在水中的全部倒影MK,若河岸高出水面的高度DE为0.75m,电线杆高为4.5m,求河宽EM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②④⑤ | B. | ②③④⑤ | C. | ②④⑤ | D. | ①③⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
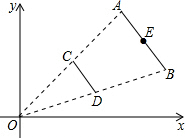 如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为( )
如图,线段CD两个端点的坐标分别为C(3,3),D(4,1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的两倍,得到线段AB,则线段AB的中点E的坐标为( )| A. | (6,6) | B. | ($\frac{7}{2}$,2) | C. | (7,4) | D. | (8,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段AB两端点的坐标分别为A(4,4)、B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C的坐标为( )
如图,线段AB两端点的坐标分别为A(4,4)、B(6,2),以原点O为位似中心,在第一象限内将线段AB缩小为原来的$\frac{1}{2}$后得到线段CD,则端点C的坐标为( )| A. | (2,1) | B. | (2,2) | C. | (1,2) | D. | (3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图所示,以O为圆心,任意长为半径画弧.与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于$\frac{1}{2}$.
如图所示,以O为圆心,任意长为半径画弧.与射线OM交于点A,再以A为圆心,AO为半径画弧,两弧交于点B,画射线OB,则cos∠AOB的值等于$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com