
分析 先由两个函数联立方程组求得到交点坐标为,再根据第三象限点的坐标特征得到不等式组,求得解集即可.
解答 解:根据题意得$\left\{\begin{array}{l}{y=2x+1}\\{y=3x+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1-b}\\{y=3-2b}\end{array}\right.$,
所以直线y=2x+1和y=3x+b的交点坐标为(1-b,3-2b),
∵交点在第三象限,
∴$\left\{\begin{array}{l}{1-b<0}\\{3-2b<0}\end{array}\right.$,
解得b>$\frac{3}{2}$,
即b的取值范围为b>$\frac{3}{2}$.
点评 本题考查了两直线平行或相交的问题:直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)平行,则k1=k2;若直线y=k1x+b1(k1≠0)和直线y=k2x+b2(k2≠0)相交,则交点坐标满足两函数的解析式.也考查了解一元一次不等式.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
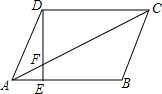 如图,平行四边形ABCD中,点E在AB边上,AE:EB=1:2,连结DE、AC交于点F,CF:CA=3:4;平行四边形被分成的4部分的面积比为1:3:9:11(从小到大).
如图,平行四边形ABCD中,点E在AB边上,AE:EB=1:2,连结DE、AC交于点F,CF:CA=3:4;平行四边形被分成的4部分的面积比为1:3:9:11(从小到大).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
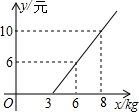 汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需要购买行李票,行李费用y(元)与行李质量x(kg)之间函数关系的图象如图所示.
汽车客运公司规定旅客可随身携带一定质量的行李,若超过规定,则需要购买行李票,行李费用y(元)与行李质量x(kg)之间函数关系的图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:等腰直角三角形ABC在平面直角坐标系中,点C坐标为(-6,8),AC=BC,∠ACB=90°,点A,B在x轴上,BC交y轴于点D,连接AD.
如图:等腰直角三角形ABC在平面直角坐标系中,点C坐标为(-6,8),AC=BC,∠ACB=90°,点A,B在x轴上,BC交y轴于点D,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | $\frac{1}{{2}^{n-1}}$ | B. | $\frac{1}{{2}^{n}}$ | C. | 3-$\frac{1}{{2}^{n}}$ | D. | $\frac{3}{{2}^{n}}$-$\frac{1}{{2}^{n+1}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com