
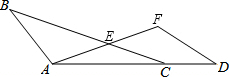
 如图,点A,C,D在同一条直线上,BC与AF交于点E,AF=AC,AD=BC,AE=EC.
如图,点A,C,D在同一条直线上,BC与AF交于点E,AF=AC,AD=BC,AE=EC.分析 (1)根据SAS即可证明;
(2)利用全等三角形的性质,求出∠BAC,根据∠BCD=∠B+∠BAC即可解决问题;
解答 (1)证明:∵EA=EC,
∴∠EAC=∠ECA,
在△AFD和△CAB中,
$\left\{\begin{array}{l}{AF=CA}\\{∠FAD=∠BCA}\\{AD=CB}\end{array}\right.$,
∴△AFD≌△CAB,
∴FD=AB.
(2)解:∵△AFD≌△CAB,'
∴∠BAC=∠F=110°,
∴∠BCD=∠B+∠BAC=50°+110°=160°.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
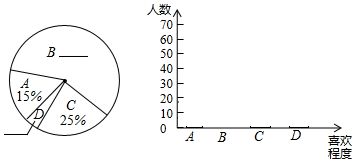 某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表.
某校为了进一步改变本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查,我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A.非常喜欢”、“B.比较喜欢”、“C.不太喜欢”、“D.很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下三幅不完整的统计图表. | 喜欢程度 | 频数 |
| A | 18 |
| B | 66 |
| C | 30 |
| D | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
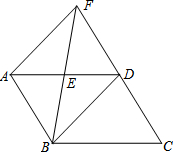 如图,?ABCD中,E为AD的中点,直线BE、CD相交于点F.连接AF、BD.
如图,?ABCD中,E为AD的中点,直线BE、CD相交于点F.连接AF、BD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
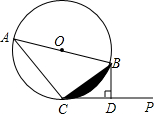 已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.
已知:AB是⊙O的直径,直线CP切⊙O于点C,过点B作BD⊥CP于D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+6的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(x<0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,且OB:OA:OD=6:3:2
如图,一次函数y=kx+6的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=$\frac{n}{x}$(x<0)的图象在第二象限交于点C,CD⊥x轴,垂足为D,且OB:OA:OD=6:3:2查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com