
| 种树、种草每亩每年补粮补钱情况表 | ||
| 种树 | 种草 | |
| 补粮 | 150千克 | 100千克 |
| 补钱 | 200元 | 150元 |
分析 (1)去年种树x亩,种草y亩,共30亩地,共补粮4000千克列方程组求解即可;
(2)设今年增加z亩种树,则增加(30-z)亩种草,根据政府补钱不少于12000元列不等式求解即可.
解答 解:(1)去年种树x亩,种草y亩.
根据题意得:$\left\{\begin{array}{l}{x+y=30}\\{150x+100y=4000}\end{array}\right.$,
解得:x=20,y=10.
答:去年种树20亩,种草10亩.
(2)设今年增加z亩种树,则增加(30-z)亩种草.
根据题意得:200(20+z)+150(30-z+10)≥12000,
解得:z≥10.
答:至少需要增加安排10亩山坡种树.
点评 本题主要考查的是一元一次不等式、二元一次方程组的应用,根据题意列出方程或不等式是解题的关键.


 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
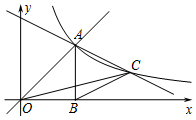 如图,直线y=x与反双曲线y=$\frac{k}{x}$(k>0)在第一象限交于点A,AB⊥x轴于B(2,0),点C是双曲线y=$\frac{k}{x}$(k>0)图象上一动点.
如图,直线y=x与反双曲线y=$\frac{k}{x}$(k>0)在第一象限交于点A,AB⊥x轴于B(2,0),点C是双曲线y=$\frac{k}{x}$(k>0)图象上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
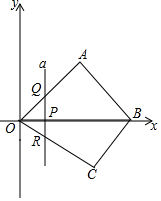 如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A在第一象限,点C在第四象限,点B在x轴的正半轴上,∠OAB=90°且OA=AB,OB=6,OC=5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com