
 ��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�C����F��CD��һ�㣬������$\frac{CF}{FD}$=$\frac{1}{3}$������AF���ӳ�����O�ڵ�E������AD��DE����CF=2��AF=3���������н��ۣ�
��ͼ��AB�ǡ�O��ֱ������CD��AB�ڵ�C����F��CD��һ�㣬������$\frac{CF}{FD}$=$\frac{1}{3}$������AF���ӳ�����O�ڵ�E������AD��DE����CF=2��AF=3���������н��ۣ�| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
���� �ɴ��������ó�CG=DG��$\widehat{AC}$=$\widehat{AD}$���ó�Բ�ܽǡ�ADF=��E�����ɹ�������ȣ����ɵó���ADF�ס�AED������ȷ��
����֪�������FD���ó�CD��CG���������FG=2���ڴ���
���ཻ�Ҷ������EF���ó�AE���ɡ�ADF�ס�AED���ó���Ӧ�߳ɱ���$\frac{AD}{AE}$=$\frac{AF}{AD}$�����AD2=21���ɹ��ɶ������AG���ó�tan��E=tan��ADF=$\frac{AG}{DG}$=$\frac{\sqrt{5}}{2}$������ȷ��
���������ε������ʽ���ɵõ�S��ADF=3$\sqrt{5}$���ܴ���
��� �⣺��AB�ǡ�O��ֱ������CD��AB��
��CG=DG��$\widehat{AC}$=$\widehat{AD}$����AGF=��AGD=90�㣬
���ADF=��E��
�֡ߡ�DAF=��EAD��
���ADF�ס�AED��
�����ȷ��
��$\frac{CF}{FD}$=$\frac{1}{3}$��CF=2��
��FD=6��
��CD=8��
��CG=DG��
��CG=DG=4��
��FG=2��
��ڴ���
��AF•EF=CF•FD��
��3EF=2��6��
��EF=4��
��AE=7��
�ߡ�ADF�ס�AED��
��$\frac{AD}{AE}$=$\frac{AF}{AD}$��
��AD2=AE��AF=7��3=21��
��Rt��ADG��AG=$\sqrt{A{D}^{2}-D{G}^{2}}$=$\sqrt{21-{4}^{2}}$=$\sqrt{5}$��
��tan��E=tan��ADF=$\frac{AG}{DG}$=$\frac{\sqrt{5}}{4}$��
��۴���
��S��ADF=$\frac{1}{2}$FD•AG=$\frac{1}{2}��6��\sqrt{5}$=3$\sqrt{5}$��
��ܴ���
��ѡA��
���� ������Բ���ۺ���Ŀ��������Բ�ܽǶ��������������ε��ж������ʡ��������������ɶ������ཻ�Ҷ��������Ǻ���������������ļ����֪ʶ�������ѶȽϴ��ۺ���ǿ���ر��Ǣ��У���Ҫ�������������ơ����ɶ������ཻ�Ҷ�����Բ�ܽǶ������ܵó������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{7}$ | B�� | $\frac{2}{7}$ | C�� | $\frac{3}{7}$ | D�� | $\frac{4}{7}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
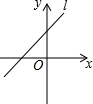 ֱ��l��y=��2-k��x+2��kΪ����������ͼ��ʾ����k��ȡֵ��Χ�������ϱ�ʾΪ��������
ֱ��l��y=��2-k��x+2��kΪ����������ͼ��ʾ����k��ȡֵ��Χ�������ϱ�ʾΪ��������| A�� |  | B�� |  | C�� | 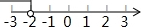 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������ABCD�У�E��BC���ϵĵ㣬AE��BD�ڵ�F����EC=2BE����$\frac{BF}{FD}$��ֵ��$\frac{1}{3}$��
��ͼ��������ABCD�У�E��BC���ϵĵ㣬AE��BD�ڵ�F����EC=2BE����$\frac{BF}{FD}$��ֵ��$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
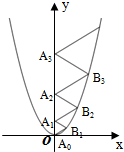 ���κ���y=$\frac{2}{3}$x2��ͼ����ͼ��ʾ����A0λ������ԭ�㣬A1��A2��A3������A2016��y����������ϣ�B1��B2��B3������B2016 �ڶ��κ���y=$\frac{2}{3}$x2��һ����ͼ���ϣ�����A0B1A1����A1B2A2����A2B3A3��������A2015B2016A2016��Ϊ�ȱ������Σ����A2015B2016A2016�ı߳�=2016��
���κ���y=$\frac{2}{3}$x2��ͼ����ͼ��ʾ����A0λ������ԭ�㣬A1��A2��A3������A2016��y����������ϣ�B1��B2��B3������B2016 �ڶ��κ���y=$\frac{2}{3}$x2��һ����ͼ���ϣ�����A0B1A1����A1B2A2����A2B3A3��������A2015B2016A2016��Ϊ�ȱ������Σ����A2015B2016A2016�ı߳�=2016���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
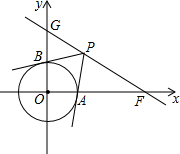 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��֪��F��2$\sqrt{3}$��0����ֱ��GF��y���������ڵ�G���ҡ�GFO=30�㣮
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��֪��F��2$\sqrt{3}$��0����ֱ��GF��y���������ڵ�G���ҡ�GFO=30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
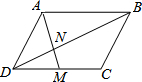 ��ͼ����ƽ���ı���ABCD�У������MΪCD���е㣬AM��BD�ཻ�ڵ�N������֪S��DMN=3����ôS��BAN���ڣ�������
��ͼ����ƽ���ı���ABCD�У������MΪCD���е㣬AM��BD�ཻ�ڵ�N������֪S��DMN=3����ôS��BAN���ڣ�������| A�� | 6 | B�� | 9 | C�� | 12 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ���ı���ABCD�У�E��AB���е㣬CE��BD���ڵ�O�����OCD�����Ϊm����OEB�����Ϊ$\sqrt{5}$�������н�������ȷ���ǣ�������
��ͼ����ƽ���ı���ABCD�У�E��AB���е㣬CE��BD���ڵ�O�����OCD�����Ϊm����OEB�����Ϊ$\sqrt{5}$�������н�������ȷ���ǣ�������| A�� | m=5 | B�� | m=4$\sqrt{5}$ | C�� | m=3$\sqrt{5}$ | D�� | m=10 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com