练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    解方程：3-
    x-1
    2
    =3x-1    ．
    考点：解一元一次方程
    专题：计算题
    分析：方程去分母，去括号，移项合并，将x系数化为1，即可求出解．
    解答：解：去分母得：6-x+1=6x-2，
    移项合并得：7x=9，
    解得：x=
    9
    7
    ．
    点评：此题考查了解一元一次方程，其步骤为：去分母，去括号，移项合并，将未知数系数化为1，求出解．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

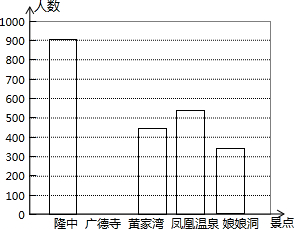    我市近年来大力发展旅游业，吸引了众多游客前来观光旅游，某旅行社对去年“五•一”假期接待的游客作了抽样调查．对本市西线的五个旅游景点的调查结果如图表：
    景点 频数 频率
    隆中 900 0.30
    广德寺 750 0.25
    黄家湾
     
    		 0.15
    凤凰温泉 540 0.18
    娘娘洞 360 0.12
    （1）此次共抽样调查了
     
    人；
    （2）请将以上图表补充完整；
    （3）今年“五•一”假期田田，丹丹和格格准备在一天内游玩两个景点，求隆中被选中的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知如图，直线AB、CD相交于点O，∠BOC与∠DOE互余，若∠AOC=108°，求∠DOE的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在?ABCD中，AE⊥BD于点E．BM⊥AC于点M，CN⊥BD于点N，DF⊥AC于点F．求证：EF∥MN．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    解答题
    （1）解不等式组
    1-
    x+1
    3
    ≥0
    3-4(x-1)＜1
    ；
    （2）解不等式
    2x-1
    3
    -
    5x+1
    2
    ≤1，并把它的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某家电商场计划用7.2万元从生产厂家购进50台电视机．已知该厂家生产3种不同型号的电视机，出厂价分别为A种每台1200元，B种每台1680元，C种每台2000元．
    （1）若家电商场同时购进两种不同型号的电视机共50台，恰好用去7.2万元，请你研究一下商场的可能进货方案．
    （2）若商场销售一台A种电视机可获利180元，销售一台B种电视机可获利240元，销售一台C种电视机可获利300元，在同时购进两种不同型号的电视机方案中，为了使销售时获利最多，你选择哪种方案？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

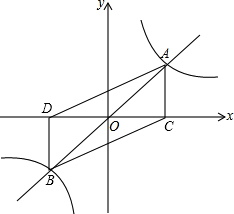    已知反比例函数y=
    k
    x
    (k＞0)    与正比例函数y=mx（m＞0）相交于A、B 两点．
    （1）分别过A，B两点向x轴作垂线，垂足分别为C，D，求证：四边形ACBD是平行四边形；
    （2）若m=1，k=2，求出线段AB的长；
    （3）若m，k分别满足 ①、②两式：
    m2-5m+1=0…①；
    关于x的方程
    5
    x-2
    -
    k
    x2-4
    =
    2
    x+2
    有增根…②
    试求：（i）m+
    1
    m
    的值    ；
    （ii） 以AB为等腰直角三角形的斜边的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

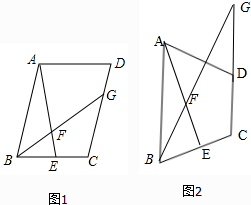    如图1，在?ABCD中，点E是BC边的中点，点F是线段AE上一点，BF的延长线交射线CD于点G．若
    AF
    EF
    =3，求
    CD
    CG
    的值．
    （1）在图1中，过点E作EH∥AB交BG于点H，则AB和EH的数量关系是
     
    ，CG与EH的数量关系是
     
    ，
    CD
    CG
    的值是
     
    ；
    （2）在原题的条件下，若
    AF
    EF
    =m（m＞0），试求
    CD
    CG
    的值（用含m的代数式表示，写出解答过程）．
    （3）如图2，在梯形ABCD中，AB∥CD，点E是BC边的中点，点F是线段AE上一点，若BF的延长线交CD于点G，且
    AF
    EF
    =m，
    CD
    AB
    =n，则
    CD
    CG
    的值是
     
    （用含m、n的代数式表示，不要求证明）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某车间有28名工人，生产一种螺栓和螺母，每人每天平均能生产螺栓12只或螺母18只，要求一个螺栓配两个螺母，应怎样分配工人才能使每天生产的螺栓和螺母恰好配套？

    查看答案和解析>>

    同步练习册答案