练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
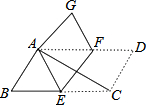
    19．在?ABCD中，∠ACB=25°，现将?ABCD沿EF折叠，使点C与点A重合，点D落在G处，则∠GFE的度数（　　）
    A．135°B．120°C．115°D．100°

    分析 首先根据折叠找到对应相等的角∠EAC=∠ECA=25°，∠FEC=∠AEF，∠DFE=∠GFE，然后根据三角形内角和可算出∠AEC，进而可得∠FEC的度数，再根据平行四边形的性质可得∠DFE=115°，进而可得答案．

    解答 解：由折叠可得：∠EAC=∠ECA=25°，∠FEC=∠AEF，∠DFE=∠GFE，
    ∵∠EAC+∠ECA+∠AEC=180°，
    ∴∠AEC=130°，
    ∴∠FEC=65°，
    ∵四边形ABCD是平行四边形，
    ∴AD∥BC，
    ∴∠DFE+∠FEC=180°，
    ∴∠DFE=115°，
    ∴∠GFE=115°，
    故选：C．

    点评 此题主要考查了平行四边形的性质，以及折叠变换，关键是找准折叠后哪些角是对应相等的．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

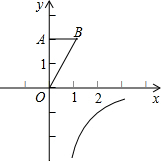    9．如图，OA在y轴上，点B在第一象限内，OA=2，OB=$\sqrt{5}$，若将△OAB绕点O顺时针方向旋转90°，此时点B恰好落在反比例函数y=$\frac{k}{x}$（x＞0）的图象上，则该反比例函数的函数关系式是y=-$\frac{2}{x}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

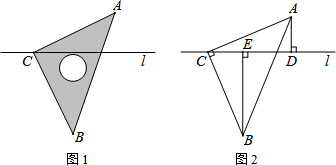
    10．如图，增加条件能判断△ACD≌△ABE的是（　　）
    A．AC=AB，AD=AEB．∠AEB=∠ADCC．AC=AB，CD=BED．∠C=∠B

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．如图，在矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE，则∠EAC为（　　）
    A．30°B．45°C．60°D．75°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．实数a、b、c在数轴上的位置如图所示，化简：$\sqrt{（a-b）^{2}}$-|a+c|+$\sqrt{（c-b）^{2}}$-|-2b|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在?ABCD中，E是AD边上的中点，连接BE并延长与CD的延长线交于点F．证明：AB=DF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．已知：如图，CD⊥AB，GF⊥AB，∠B=∠ADE，求证：∠1=∠2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．如图1，将一块等腰直角三角板ABC的直角顶点C置于直线l上，图2是由图1抽象出的几何图形，过A、B两点分别作直线l的垂线，垂足分别为D、E．
    （1）△ACD与△CBE全等吗？说明你的理由．
    （2）猜想线段AD、BE、DE之间的关系．（直接写出答案）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．若使代数式$\frac{x}{5}$-5的值不大于$\frac{x}{2}$-3的值，则x的取值范围是x≥-$\frac{20}{3}$．

    查看答案和解析>>

    同步练习册答案