
����Ŀ���ס�����̨������ͬ�ӹ�һ�������һ������![]() Сʱ���ڼӹ��������һ��������ֹͣ�������ų����Ϻ��һ�������˹���Ч���ұ��ֲ��䣬�����ӹ��������ڼӹ������й���Ч�ʱ��ֲ��䣮�ס�����̨�����ӹ����������
Сʱ���ڼӹ��������һ��������ֹͣ�������ų����Ϻ��һ�������˹���Ч���ұ��ֲ��䣬�����ӹ��������ڼӹ������й���Ч�ʱ��ֲ��䣮�ס�����̨�����ӹ����������![]() ��������ӹ�ʱ��
��������ӹ�ʱ��![]() ֮��ĺ���ͼ��Ϊ����
֮��ĺ���ͼ��Ϊ����![]() ����ͼ��ʾ��
����ͼ��ʾ��
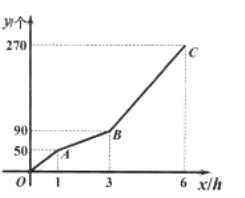
��1���������һ������ ����������ÿСʱ�ӹ��� ����������һ����ų����Ϻ�ÿСʱ�ӹ��� ���������
��2����![]() ʱ����
ʱ����![]() ��
��![]() ֮��ĺ�������ʽ��
֮��ĺ�������ʽ��
��3���������ӹ������У��ӹ��ʱ��ʱ�������Ҽӹ������������ȣ�
���𰸡���1��![]() ����2��
����2��![]()
![]() ����3���ӹ�
����3���ӹ�![]() ��
��![]() ʱ�������Ҽӹ�������������.
ʱ�������Ҽӹ�������������.
��������
(1)�۲�ͼ��ɵ�����ܸ������۲�AB�οɵü������ٶȣ��۲�BC�ν�ϼ��ٶȿ�����ҵ��ٶȣ�
(2)�赱![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�������ʽΪ
֮��ĺ�������ʽΪ![]() �����ô���ϵ������⼴�ɣ�
�����ô���ϵ������⼴�ɣ�
(3)���һ������ֹ���ǰ���ù��Ϻ���������ֱ����������⼴��.
(1)�۲�ͼ���֪һ���ӹ����270����
����ÿСʱ�ӹ������(90-50)��(3-1)=20����
�һ����ų����Ϻ�ÿСʱ�ӹ������(270-90)��(6-3)-20=40����
�ʴ�Ϊ��270��20��40��
![]() �赱
�赱![]() ʱ��
ʱ��![]() ��
��![]() ֮��ĺ�������ʽΪ
֮��ĺ�������ʽΪ![]()
��![]() ��
��![]() ���������ʽ����
���������ʽ����
![]() ���
���![]()
![]()
![]()
![]() ��ӹ�
��ӹ�![]() Сʱʱ�������Ҽӹ������������ȣ�
Сʱʱ�������Ҽӹ������������ȣ�
�һ������ֹ���ʱ�Ѽӹ����50-20=30����
![]() ��
��
![]() ��
��
�һ����ú�����������
![]() ��
��
![]() ��
��
�𣺼ӹ�![]() ��
��![]() ʱ�������Ҽӹ�������������.
ʱ�������Ҽӹ�������������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() ���ཻ��
���ཻ��![]() ���㣨��
���㣨��![]() �ڵ�
�ڵ�![]() ����ࣩ����
����ࣩ����![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() .����������һ��
.����������һ��![]() ����
����![]() .
.
��1���������ߵĽ���ʽ�Ͷ�������.
��2������![]() �
λ��![]() ���·�ʱ����
���·�ʱ����![]() ��������ֵ.
��������ֵ.
��3��������������ڵ�![]() ���
���![]() ֮�䲿�֣�����
֮�䲿�֣�����![]() �͵�
�͵�![]() ����ߵ�����͵��������֮��Ϊ
����ߵ�����͵��������֮��Ϊ![]() .��
.��![]() ����
����![]() �ĺ�������ʽ����д���Ա���
�ĺ�������ʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�ڵ�![]() ʱ����
ʱ����![]() ��������___________.
��������___________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC������D��E�ֱ��ڱ�AB��AC����DE��BC���ӳ����ཻ�ڵ�F����![]() ��
��
��1����֤![]() ��
��
��2����AB=12��AC=9��AE=8ʱ����BD�ij���![]() ��ֵ��
��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
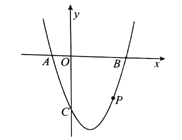
����Ŀ����ƽ��ֱ������ϵxOy�У�����P�ĺ��������������ȣ���Ƶ�PΪ�����㣮��֪���κ���![]() ��ͼ��������ֻ��һ��������
��ͼ��������ֻ��һ��������![]() ���ҵ�
���ҵ�![]() ʱ������
ʱ������![]() ����СֵΪ��3�����ֵΪ1����m��ȡֵ��Χ�ǣ�������
����СֵΪ��3�����ֵΪ1����m��ȡֵ��Χ�ǣ�������
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y��ax2+bx+c��x�ύ�ڵ�A����1��0����C��3��0������BΪ�����߶��㣬ֱ��BDΪ�����ߵĶԳ��ᣬ��D��x���ϣ�����AB��BC����ABC��90�㣬AB��y�ύ�ڵ�E������CE��

��1�������B�����겢������������ߵĽ���ʽ��
��2����PΪ��һ������������һ�����㣬���PEC�����ΪS����P�ĺ�����Ϊm����S����m�ĺ�����ϵ�䣬�����S�����ֵ��
��3����ͼ2������OB�����������Ƿ���ڵ�Q��ʹֱ��QC��ֱ��BC������ǵ��ڡ�OBD����������ֱ��д����Q�����ꣻ�������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ά��������Ȩ�ͺ���Ȩ�������ಿ�Ŷ��ҹ��캣ʵ���˳�̬��Ѳ����������ͼ������ִ��Ѳ������ĺ��ബ��ÿСʱ50������ٶ������������У���![]() ����õ���
����õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ���������1Сʱ����
�����ϣ���������1Сʱ����![]() ������ʱ��õ���
������ʱ��õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ�
�����ϣ�
��1����![]() �Ķ�����
�Ķ�����
��2����֪�ڵ���![]() ����Χ25�������а������ʺ��ബ�����������������Ƿ�ȫ��
����Χ25�������а������ʺ��ബ�����������������Ƿ�ȫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
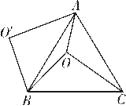
����Ŀ����ͼ��O�ǵȱߡ�ABC��һ�㣬OA=3��OB=4��OC=5�����߶�BO�Ե�BΪ��ת������ʱ����ת60��õ��߶�BO�䣬���н��ۣ�
�١�BO��A�����ɡ�BOC�Ƶ�B��ʱ����ת60��õ���&
�ڵ�O��O��ľ���Ϊ4��
�ۡ�AOB=150�㣻
���ı���AOBO������Ϊ6��3![]() ��
��
��S��AOC��S��AOB=6��![]() .
.
������ȷ�Ľ�����_______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��˫����y����![]() �ڵڶ�����֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ����������ABC���ҡ�ACB��120������C�ڵ�һ���ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����y��
�ڵڶ�����֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ����������ABC���ҡ�ACB��120������C�ڵ�һ���ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����y��![]() ���˶�����k��ֵΪ_____��
���˶�����k��ֵΪ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
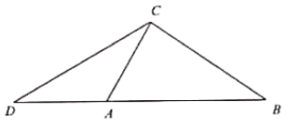
����Ŀ����ͼ����֪��![]() �У���ACB=90����
�У���ACB=90����![]() ���ӳ���BA����D��ʹAD=AC������CD.
���ӳ���BA����D��ʹAD=AC������CD.
��1�����D������ֵ��
��2��ȡ��AC���е�E������BE���ӳ�����CD�ڵ�F����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com