Question

6．在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限内，斜靠在两坐标轴上，且点A（0，2），点C（-1，0），如图所示：抛物线y=ax²+ax-5经过点B．
（1）求点B的坐标；
（2）求抛物线的解析式；
（3）在抛物线上是否还存在点P，使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．

Answer 1

分析 （1）根据题意，过点B作BD⊥x轴，垂足为D；根据角的互余的关系，易得B到x、y轴的距离，即B的坐标；
（2）根据抛物线过B点的坐标，可得a的值，进而可得其解析式；
（3）首先假设存在，分A、C是直角顶点两种情况讨论，根据全等三角形的性质，可得答案．

解答 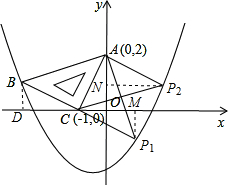解：（1）过点B作BD⊥x轴，垂足为D，
∵∠BCD+∠ACO=90°，∠ACO+∠CAO=90°，
∴∠BCD=∠CAO，
在△BCD和△CAO中，
$\left\{\begin{array}{l}{∠BCD=∠CAO}\\{∠BDC=∠COA=90°}\\{CB=AC}\end{array}\right.$，
∴△BCD≌△CAO（AAS），
∴BD=OC=1，CD=OA=2，
∴点B的坐标为（-3，1）；

（2）抛物线y=ax²+ax-5经过点B（-3，1），
则得到1=9a-3a-5，
解得a=1．
所以抛物线的解析式为y=x²+x-5；

（3）假设存在点P，使得△ACP仍然是以AC为直角边的等腰直角三角形：
①若以点C为直角顶点；
则延长BC至点P₁，使得P₁C=BC，得到等腰直角三角形△ACP₁，
过点P₁作P₁M⊥x轴，
∵CP₁=BC，∠MCP₁=∠BCD，∠P₁MC=∠BDC=90°，
∴△MP₁C≌△DBC．
∴CM=CD=2，P₁M=BD=1，可求得点P₁（1，-1）；
②若以点A为直角顶点；
则过点A作AP₂⊥CA，且使得AP₂=AC，得到等腰直角三角形△ACP₂，
过点P₂作P₂N⊥y轴，同理可证△AP₂N≌△CAO，
∴NP₂=OA=2，AN=OC=1，可求得点P₂（2，1），
③以A为直角顶点的等腰Rt△ACP的顶点P有两种情况．即过点A作直线L⊥AC，在直线L上截取AP=AC时，点P可能在y轴右侧，即现在解答情况②的点P₂；
点P也可能在y轴左侧，即还有第③种情况的点P₃．因此，然后过P₃作P₃G⊥y轴于G，同理：△AGP₃≌△CAO，
∴GP₃=OA=2，AG=OC=1，
∴P₃为（-2，3）；
经检验，点P₂（2，1）在抛物线y=x²+x-5上，点P₁（1，-1）与点P₃（-2，3）不在抛物线上．
∴符合条件的点只有一个：P（2，1）．

点评 本题考查学生将二次函数的图象与解析式相结合处理问题、解决问题的能力，综合性强，能力要求极高．考查学生分类讨论，数形结合的数学思想方法．