
| 2 |

| ||
| 2 |
| 2 |
| 2 |
5
| ||
| 2 |
| 5 |
| 2 |
| ||
| 3 |
7
| ||
| 3 |
14
| ||
| 3 |
7
| ||
| 3 |
| 51 |
| 16 |
21
| ||
| 16 |
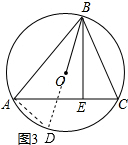
 作直径BD,BH⊥AC于H,连结AD,如图1,
作直径BD,BH⊥AC于H,连结AD,如图1,
| ||
| 2 |
| ||
| 2 |
| 2 |
| AH2+BH2 |
| 2 |
| 2 |
5
| ||
| 2 |

| 5 |
| 2 |
| 5 |
| 2 |
| ||
| 3 |
7
| ||
| 3 |
14
| ||
| 3 |
7
| ||
| 3 |
| 51 |
| 16 |
| 51 |
| 16 |
| BC2-CE2 |
21
| ||
| 16 |
| AD |
| BC |
| AB |
| AE |
| 6×7 | ||||
|
32
| ||
| 15 |
16
| ||
| 15 |


科目:初中数学 来源: 题型:
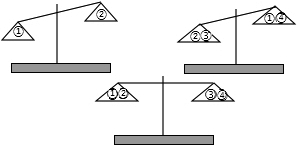 小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)
小雨的爸爸从市场买回来四个大西瓜,爸爸为了考一考小雨,让小雨把四个大西瓜依次边上①,②,③,④号后,按质量由小到大的顺序排列出来(不准用称),小雨用一个简易天平操作,操作如下:(操作过程中,天平自身损坏忽略不计)查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
| A、4个 | B、3个 | C、2个 | D、1个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com