
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,E是AB上一点,连接CE,现将
,E是AB上一点,连接CE,现将![]() 向上方翻折,折痕为CE,使点B落在点P处.
向上方翻折,折痕为CE,使点B落在点P处.

(1)当点P落在CD上时,![]() _____;当点P在矩形内部时,BE的取值范围是_____.
_____;当点P在矩形内部时,BE的取值范围是_____.
(2)当点E与点A重合时:①画出翻折后的图形(尺规作图,保留作图痕迹);②连接PD,求证:![]() ;
;

(3)如图,当点Р在矩形ABCD的对角线上时,求BE的长.

【答案】(1)12,0<BE<12;(2)①见解析,②见解析;(3)6或9.
【解析】
(1)由折叠的性质得到推出△BCE是等腰直角三角形,即可得到结论;
(2)①由题意画出图形即可;
②根据全等三角形的性质得到∠PAC=∠DCA,设AP与CD相交于O,于是得到OA=OC,求得∠OAC=∠OPD,根据平行线的判定定理得到结论;
(3)分两种情形,当点P在对角线AC或对角线BD上时,两种情形分别求解即可.
解:(1)当点P在CD上时,如图1,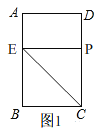
∵将∠B向右上方翻折,折痕为CE,使点B落在点P处,
∴∠BCE=∠ECP=45°,
∴△BCE是等腰直角三角形,
∴BE=BC=AD=12,
当点P在矩形内部时,BE的取值范围是0<BE<12;
故答案为:12,0<BE<12;
(2)①补全图形如图2所示,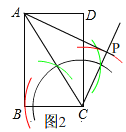
②当点E与点A重合时,如图3,连接PD,设CD交PA于点O.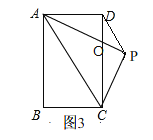
由折叠得,AB=AP=CD,
在△ADC与△CPA中,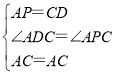 ,
,
∴△ADC≌△CPA,
∴∠PAC=∠DCA,
设AP与CD相交于O,则OA=OC,
∴OD=OP,∠ODP=∠OPD,
∵∠AOC=∠DOP,
∴∠OAC=∠OPD
∴PD∥AC;
(3)如图4中,当点P落在对角线AC上时,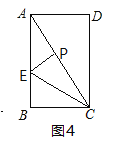
由折叠得,BC=PC=12,AC=![]() =20,
=20,
∴PA=8,设BE=PE=x,
在Rt△APE中,(16-x)2=x2+82,
解得x=6.
∴BE=6.
如图5中,当点P落在对角线BD上时,设BD交CE于点M.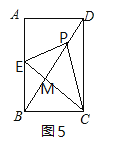
由折叠得,BE=PE,∠BEC=∠PEC,
∵EM=EM,
∴△MBE∽△MEP,
∴∠EMB=∠EMP,
∵∠EMB+∠EMP=180°,
∴EC⊥BD,
∴∠BCE=∠ABD,
∵∠A=∠ABC=90°,
∴△CBE∽△BAD,
∴![]() ,
,
∴![]() ,
,
∴BE=9,
综上所述,满足条件的BE的值为6或9.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
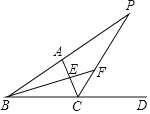
【题目】如图,已知BE是△ABC的角平分线,CP是△ABC的外角∠ACD的平分线.延长BE,BA分别交CP于点F,P.
(1)求证:∠BFC![]() ∠BAC;
∠BAC;
(2)小智同学探究后提出等式:∠BAC=∠ABC+∠P.请通过推理演算判断“小智发现”是否正确?
(3)若2∠BEC﹣∠P=180°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下表从左到右在毎个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等,则第2017个格子中的数字是( )
3 |
|
|
| -1 | 2 | …… |
A.3B.2C.0D.-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在一次环保知识宣传活动中,需要印刷若干份调查问卷。印刷厂有甲、乙两种收费方式:甲种方式收制版费6元,每一份收印刷费0.1元;乙种方式不收制版费,每印一份收印刷费0.12元。设共印调查问卷![]() 份:
份:
(1)按甲种方式应收费多少元,按乙种方式应收费多少元(用含![]() 的代数式表示);
的代数式表示);
(2)若共需印刷500份调查问卷,通过计算说明选用哪种方式合算?
(3)印刷多少份调查问卷时,甲、乙两种方式收费一样多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知抛物线的顶点坐标为(2,0),且经过点(4,1),如图,直线y=![]() x与抛物线交于A、B两点,直线l为y=﹣1.
x与抛物线交于A、B两点,直线l为y=﹣1.
(1)求抛物线的解析式;
(2)在l上是否存在一点P,使PA+PB取得最小值?若存在,求出点P的坐标;若不存在,请说明理由.
(3)知F(x0,y0)为平面内一定点,M(m,n)为抛物线上一动点,且点M到直线l的距离与点M到点F的距离总是相等,求定点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=90°,AC=4cm,BC=3cm若动点![]() 从点
从点![]() 开始,按
开始,按![]() 的路径运动,且速度为每秒1cm,设运动的时间为x秒.
的路径运动,且速度为每秒1cm,设运动的时间为x秒.
(1)当x=__ __秒 时,CP把△ABC的面积分成相等的两部分,并求出此时CP=__ __cm;
(2)当x为何值时,△ABP为等腰三角形?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com