
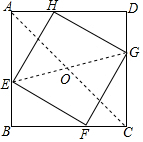
 如图,正方形ABCD的边长为10cm,E,F,G,H分别是AB,BC,CD,DA上的点,且AE=BF=CG=DH.
如图,正方形ABCD的边长为10cm,E,F,G,H分别是AB,BC,CD,DA上的点,且AE=BF=CG=DH.分析 (1)由正方形的性质得出∠BAD=∠B=∠BCD=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出结论;
(2)连接AC、EG,交点为O;先证明△AOE≌△COG,得出OA=OC,证出O为对角线AC、BD的交点,即O为正方形的中心;
(3)设四边形EFGH面积为S,BE=xcm,则BF=(10-x)cm,由勾股定理得出S=x2+(10-x)2=2(x-5)2+50,S是x的二次函数,容易得出x=5时,四边形EFGH的面积最小.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠BAD=∠B=∠BCD=∠D=90°,AB=BC=CD=DA,
∵AE=BF=CG=DH,
∴AH=BE=CF=DG,
在△AEH、△BFE、△CGF和△DHG中,$\left\{\begin{array}{l}{AE=BF=CG=DH}&{\;}\\{∠BAD=∠B=∠BCD=∠D}&{\;}\\{AH=BE=CF=DG}&{\;}\end{array}\right.$,
∴△AEH≌△BFE≌△CGF≌△DHG(SAS),
∴EH=FE=GF=GH,∠AEH=∠BFE,
∴四边形EFGH是菱形,
∵∠BEF+∠BFE=90°,
∴∠BEF+∠AEH=90°,
∴∠HEF=90°,
∴四边形EFGH是正方形;
(2)解:直线EG经过一个定点,这个定点为正方形的中心(AC、BD的交点);理由如下:
连接AC、EG,交点为O;如图所示: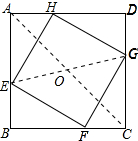 ∵四边形ABCD是正方形,
∵四边形ABCD是正方形,
∴AB∥CD,
∴∠OAE=∠OCG,
在△AOE和△COG中,$\left\{\begin{array}{l}{∠OAE=∠OCG}&{\;}\\{∠AOE=∠COG}&{\;}\\{AE=CG}&{\;}\end{array}\right.$,
∴△AOE≌△COG(AAS),
∴OA=OC,OE=OG,
即O为AC的中点,
∵正方形的对角线互相平分,
∴O为对角线AC、BD的交点,即O为正方形的中心;
(3)解:设四边形EFGH面积为S,设BE=xcm,则BF=(10-x)cm,
根据勾股定理得:EF2=BE2+BF2=x2+(10-x)2,
∴S=x2+(10-x)2=2(x-5)2+50,
∵2>0,
∴S有最小值,
当x=5时,S的最小值=50,
即E点是AB的中点时,四边形EFGH面积的最小值为50cm2.
点评 本题是四边形综合题目,考查了正方形的性质与判定、菱形的判定、全等三角形的判定与性质、勾股定理、二次函数的最值等知识;本题综合性强,有一定难度,特别是(2)(3)中,需要通过作辅助线证明三角形全等和运用二次函数才能得出结果.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:初中数学 来源: 题型:解答题
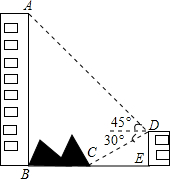 如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=50m,DE=10m,求障碍物B,C两点间的距离(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
如图,大楼AB右侧有一障碍物,在障碍物的旁边有一幢小楼DE,在小楼的顶端D处测得障碍物边缘点C的俯角为30°,测得大楼顶端A的仰角为45°(点B,C,E在同一水平直线上),已知AB=50m,DE=10m,求障碍物B,C两点间的距离(结果精确到1m,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
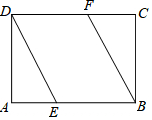 如图,E、F分别是矩形ABCD的边AB、CD上一点,且AE=CF,连接BF、DE.
如图,E、F分别是矩形ABCD的边AB、CD上一点,且AE=CF,连接BF、DE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )
如图,在等腰直角三角形ABC中,直角边AB=AC=4,以AB为直径的半圆交斜边BC于点D,则图中阴影部分的面积为(结果保留π)( )| A. | 6-π | B. | 8-π | C. | 8-2π | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4.5元 | B. | 4元 | C. | 3.5元 | D. | 3元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com