
分析 (1)根据勾股定理求出AB的长即可解决问题.
(2)分三种情形①如图2中,当0≤t≤4时,重叠部分是△OMF,作MN⊥OF,BK⊥OC于K.②如图3中,当4<t≤10时,重叠部分是四边形MNEF.③如图4中,当10<t≤14时,重叠部分是△MEC.分别求解即可.
(3)分四种情形①如图5中,当ON=OM时,作OH⊥BC于H.根据sin∠BNE′=sin∠BOH=$\frac{DE′}{DN}$=$\frac{\sqrt{5}}{5}$,求解.②如图6中,当MO=MN时,根据sin∠DNE′=sin∠BOC=$\frac{DE′}{DN}$=求解.③如图7中,当OM=ON时,作OG⊥BC于G,交MN于H,根据sin∠DNE′=sin∠BOG=$\frac{DE′}{DN}$=$\frac{OG}{OB}$求解.④如图8中,当NO=NM时,作B关于y轴的对称点G,连接GO,作GH⊥OD于H.由△GHO∽△DE′N,得$\frac{DN}{GO}$=$\frac{DE′}{GH}$,列出方程即可解决.
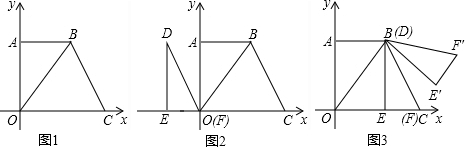
解答 解:(1)如图1中,
在Rt△OAB中,∵∠OAB=90°,OA=8,OB=OC=10,
∴AB=$\sqrt{O{B}^{2}-O{A}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴点B坐标(6,8).
(2)①如图2中,当0≤t≤4时,重叠部分是△OMF,作MN⊥OF,BK⊥OC于K.
∵DE=BK,EF=KC,∠DEF=∠BKC=90°,
∴△DEF≌△BKC,
∴∠DFE=∠BCK,
∴DF∥BC,
∴△OMF∽△OBC,
∴$\frac{OF}{OC}$=$\frac{MN}{BK}$,
∴$\frac{t}{10}$=$\frac{MN}{8}$,
∴MN=$\frac{4}{5}$t,
∴S=$\frac{1}{2}$•t•$\frac{4}{5}$t=$\frac{2}{5}$t2.
②如图3中,当4<t≤10时,重叠部分是四边形MNEF,
S=S△OMF-S△ONE=$\frac{2}{5}$t2-$\frac{1}{2}$•(t-4)•$\frac{4}{3}$•(t-4)=-$\frac{4}{15}$t2+$\frac{16}{3}$t-$\frac{32}{3}$
③如图4中,当10<t≤14时,重叠部分是△MEC.
由$\frac{ME}{BK}$=$\frac{CE}{CK}$,可得ME=28-2t,
S=$\frac{1}{2}$•EC•ME=$\frac{1}{2}$•(14-t)•(28-2t)=t2-28t+196.
综上所述S=$\left\{\begin{array}{l}{\frac{2}{5}{t}^{2}}&{(0≤t≤4)}\\{-\frac{4}{15}{t}^{2}+\frac{16}{3}t-\frac{32}{3}}&{(4<t≤10)}\\{{t}^{2}-28t+196}&{(10<t≤14)}\end{array}\right.$
(3)存在.①如图5中,当ON=OM时,作OH⊥BC于H.
∵OB=OC,OH⊥BC,
∴∠BOH=∠HOC,
∵OM=ON,
∴∠ONM=∠OMN,
∠BOC=∠ONM+∠OMN,
∴∠BOH=∠BNE′,
∴sin∠BNE′=sin∠BOH=$\frac{DE′}{DN}$=$\frac{\sqrt{5}}{5}$,
∴DN=8$\sqrt{5}$.
②如图6中,当MO=MN时,
由sin∠DNE′=sin∠BOC=$\frac{DE′}{DN}$=$\frac{4}{5}$,
∴$\frac{8}{DN}$=$\frac{4}{5}$,
∴DN=10.
③如图7中,当OM=ON时,作OG⊥BC于G,交MN于H,
由sin∠DNE′=sin∠BOG=$\frac{DE′}{DN}$=$\frac{OG}{OB}$,
∴$\frac{8}{DN}$=$\frac{4\sqrt{5}}{10}$,
∴DN=4$\sqrt{5}$.
④如图8中,当NO=NM时,作B关于y轴的对称点G,连接GO,作GH⊥OD于H.
∵$\frac{1}{2}$•BG•AO=$\frac{1}{2}$•OB•GH,
∴GH=$\frac{48}{5}$,
由△GHO∽△DE′N,得$\frac{DN}{GO}$=$\frac{DE′}{GH}$,
∴$\frac{DN}{10}$=$\frac{8}{\frac{48}{5}}$,
∴DN=$\frac{25}{3}$,
综上所述,当△OMN是等腰三角形时,DN的长为8$\sqrt{5}$或10或4$\sqrt{5}$或$\frac{25}{3}$.
点评 本题考查几何变换综合题、解直角三角形、勾股定理、等腰三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会分类讨论,注意不能漏解,学会画好图象解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | -1≤a<0 | B. | -1<a≤0 | C. | -1≤a≤0 | D. | -1<a<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
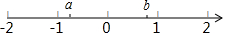 实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$-$\sqrt{(b-1)^{2}}$-$\sqrt{(a-b)^{2}}$.
实数a,b在数轴上的位置如图所示,化简:$\sqrt{(a+1)^{2}}$-$\sqrt{(b-1)^{2}}$-$\sqrt{(a-b)^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
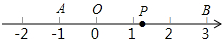 已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为X.
已知数轴上两点A、B对应的数分别为-1、3,点P为数轴上一动点,其对应的数为X.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-x+y)(-x-y) | B. | (a-2b)(2b-a) | C. | (a-b)(a+b)(a2+b2) | D. | (a-b+c)(a+b-c) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com