
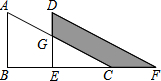
 如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$.
如图,△ABC中,∠B=90°,AB=6,将△ABC平移至△DEF的位置,若四边形DGCF的面积为15,且DG=4,则CF=$\frac{15}{4}$. 分析 根据平移的性质可知:AB=DE,设BE=CF=x;由此可求出EH和CF的长.由于CH∥DF,可得出△ECH∽△EFD,根据相似三角形的对应边成比例,可求出EC的长.已知EH、EC,DE、EF的长,即可求出△ECH和△EFD的面积,进而可根据阴影部分的面积求得x的值即可.
解答 解:根据题意得,DE=AB=6;
设BE=CF=x,
∵CH∥DF.
∴EG=6-4=2;
EG:GD=EC:CF,
即 2:4=EC:x,
∴EC=$\frac{1}{2}$x,
∴EF=EC+CF=$\frac{3}{2}$x,
∴S△EFD=$\frac{1}{2}$×$\frac{3}{2}$x×6=$\frac{9}{2}$x;
S△ECG=$\frac{1}{2}$×2×$\frac{1}{2}$x=$\frac{1}{2}$x.
∴S阴影部分=$\frac{9}{2}$x-$\frac{1}{2}$x=15.
解得:x=$\frac{15}{4}$.
故答案为$\frac{15}{4}$.
点评 此题考查平移的性质、相似三角形的判定与性质及有关图形的面积计算,有一定的综合性.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
| A. | 48 | B. | 56 | C. | 61 | D. | 63 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直线y1经过一、三、四象限 | |
| B. | 抛物线y2必经过点(1,0) | |
| C. | 当x>1或x<0时,y2>y1 | |
| D. | 当x>-1时,y1、y2均随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在菱形ABCD中,对角线AC和BD相交于点O,点E是BC的中点,连结AE,若
如图,在菱形ABCD中,对角线AC和BD相交于点O,点E是BC的中点,连结AE,若查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )
规定:如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点B的极坐标应记为( )| A. | (2$\sqrt{3}$,30°) | B. | (60°,2$\sqrt{3}$) | C. | (30°,4) | D. | (30°,2$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
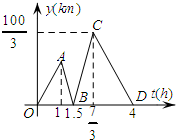 甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题:
甲开汽车,乙骑自行车从M地出发沿一条公路匀速前往N地,乙先出发一段时间后甲才出发,设乙行驶的时间为t(h),甲乙两人之间的距离为y(km),y与t的函数关系如图1所示,其中点C的坐标为($\frac{7}{3},\frac{100}{3}$),请解决以下问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com