
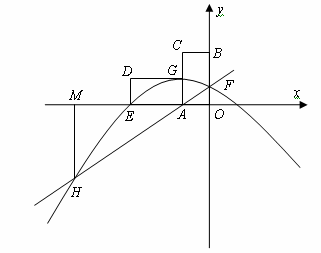
如图,点O是坐标原点,点A(n,0)是x轴上一动点(n<0)。以AO为一边作矩形AOBC,使OB=2OA,点C在第二象限。将矩形AOBC绕点A逆时针旋转90°得矩形AGDE。过点A得直线y=kx+m(k≠0)交y轴于点F,FB=FA。抛物线y=ax2+bx+c过点E、F、G且和直线AF交于点H,过点H作x轴的垂线,垂足为点M。
(1)求k的值;
(2)点A位置改变使,△AMH的面积和矩形AOBC的面积比是否改变?说明你的理由。
答案:
(1)根据题意,得B(0,-2n),当x=0时,y=kx+m=m,∴点F的坐标为(0,m).而FB=-2n-m,在Rt△AOF中,由勾股定理得,m2+n2=(-2n-m)2.化简得m=-0.75n,由于y=kx-0.75n过点A(n,0),∴0=kn-0.75n,∴k=0.75.
(2)∵抛物线y=ax2+bx+c过点E(3n,0),点F(0,-0.75n),点G(n,-n),代入解析式得y=![]() x2-
x2-![]() x-
x-![]() n.与直线组成方程组,解得H(5n,3n),HM=-3n,AM=-4n,∴△AMH的面积为6n2,而矩形AOBC的面积为2n2,∴△AMH的面积与矩形AOBC的面积的比为3,不随着点A位置的改变而改变.
n.与直线组成方程组,解得H(5n,3n),HM=-3n,AM=-4n,∴△AMH的面积为6n2,而矩形AOBC的面积为2n2,∴△AMH的面积与矩形AOBC的面积的比为3,不随着点A位置的改变而改变.
本题是一个综合性较强的题目,探索变化过程中的不变量,关键是将点的坐标用参数n来表示,进而将线段用参数n表示,注意表示过程中n<0这一条件. |


科目:初中数学 来源: 题型:
 +c过点E、F、G且和直线AF交于点H,过点H作HM⊥x轴,垂足为点M.
+c过点E、F、G且和直线AF交于点H,过点H作HM⊥x轴,垂足为点M.查看答案和解析>>
科目:初中数学 来源: 题型:
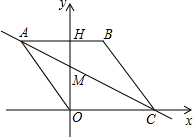 轴上,直线AC交y轴于点M,AB边交y轴于点H.
轴上,直线AC交y轴于点M,AB边交y轴于点H.| 1 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 轴上,直线AC交y轴于点M,AB边交y轴于点H.
轴上,直线AC交y轴于点M,AB边交y轴于点H. x2-bx+c经过A、O两点,求抛物线的解析式,并验证点C是否在抛物线上;
x2-bx+c经过A、O两点,求抛物线的解析式,并验证点C是否在抛物线上;查看答案和解析>>
科目:初中数学 来源:第23章《二次函数与反比例函数》中考题集(41):23.5 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2006年湖北省宜昌市中考数学试卷(课标卷)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com